MWR Fundamentals
Contents |
1 Fundamentals of radiative transfer
The basic ideas of radiative transfer and thermal emission are described described for example by Goody and Yung (1995) and Bohren and Clothieaux (2006). Their application to microwave radiometric remote sensing is outlined in Janssen (1993) and Petty (2006).
1.1 Emission
An ideal blackbody absorbs all incident radiation and re-emits all of the absorbed radiation as a function of its temperature and frequency. The spectral distribution of a blackbody emission at temperature  and frequency
and frequency 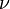 .
. 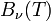 can be calculated from Planck’s law to
can be calculated from Planck’s law to
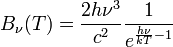
where 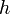 is the Planck’s constant and
is the Planck’s constant and 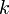 is Boltzman’s constant. This radiance expresses the emitted power per unit projected area, per unit solid angle and per unit frequency. Note the higher the temperature, the higher the emitted radiation. Most emitters however, show a lower emission compared to that of a blackbody at the same temperature, i.e. the so called “grey” body. If the fraction of incident energy from a certain direction absorbed by the grey body is
is Boltzman’s constant. This radiance expresses the emitted power per unit projected area, per unit solid angle and per unit frequency. Note the higher the temperature, the higher the emitted radiation. Most emitters however, show a lower emission compared to that of a blackbody at the same temperature, i.e. the so called “grey” body. If the fraction of incident energy from a certain direction absorbed by the grey body is 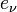 , then the amount emitted is
, then the amount emitted is 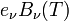 . For a perfectly reflecting or transmitting body
. For a perfectly reflecting or transmitting body 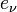 is zero and incident energy may be redirected or pass through the body without being absorbed. For an upward-looking radiometer viewing a non-scattering medium, the equation that relates the actually observed radiance
is zero and incident energy may be redirected or pass through the body without being absorbed. For an upward-looking radiometer viewing a non-scattering medium, the equation that relates the actually observed radiance 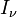 to the atmospheric state is the radiative transfer equation (RTE) (Janssen, 1993)
to the atmospheric state is the radiative transfer equation (RTE) (Janssen, 1993)
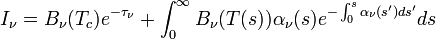
where  is path length in m,
is path length in m, 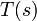 is the temperature in K at point s,
is the temperature in K at point s, 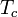 the cosmic background brightness temperature of 2.75 K,
the cosmic background brightness temperature of 2.75 K, 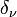 the opacity or total optical depth:
the opacity or total optical depth:
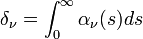
where 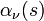 = absorption coefficient (1/m) at point
= absorption coefficient (1/m) at point  . The use of the blackbody source function is justified by the assumption of local thermodynamic equilibrium in which the population of emitting energy states is determined by molecular collisions and is independent of the incident radiation field. For a plane parallel atmosphere,
. The use of the blackbody source function is justified by the assumption of local thermodynamic equilibrium in which the population of emitting energy states is determined by molecular collisions and is independent of the incident radiation field. For a plane parallel atmosphere,  and the height
and the height 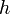 are related by
are related by 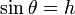 , where
, where 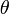 is the elevation angle of the measurement. In oder to simplify the unit of measurement, Planck's law can be solved for
is the elevation angle of the measurement. In oder to simplify the unit of measurement, Planck's law can be solved for  . In case of a "grey" emitter
. In case of a "grey" emitter  will not be identical to the physical temperature of the emitter. Thus, this temperature is defined as the (Planck-equivalent) brightness temperature
will not be identical to the physical temperature of the emitter. Thus, this temperature is defined as the (Planck-equivalent) brightness temperature 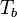 . Using this definition, the RTE becomes
. Using this definition, the RTE becomes
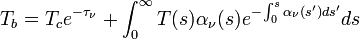
Note that 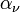 is a function of pressure, temperature, water vapor and cloud liquid. Information on the meteorological variables is obtained from measurements of
is a function of pressure, temperature, water vapor and cloud liquid. Information on the meteorological variables is obtained from measurements of 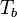 as a function of
as a function of 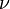 and/or
and/or 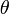 .
.
1.2 Scattering
For frequencies below 100 GHz scattering by small atmospheric particles, i.e. molecules, aerosols and cloud droplets can be neglected. However, for larger precipitating particles scattering effects need to be taken into account. For an upward-looking microwave radiometer the RTE approximation from the former section can be generalized to (e.g., Deirmendjian, 1969; Gasiewski, 1993; Marzano et al., 2002):
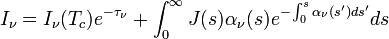
where the pseudo-source function 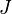 is given by
is given by
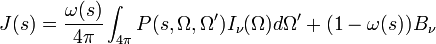
with 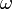 the single scattering albedo,
the single scattering albedo, 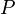 the scattering phase function (normalized to 1) and
the scattering phase function (normalized to 1) and 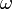 the solid angle. The scattering term of the radiative transfer equation needs to be used for precipitation remote sensing, e.g. Marzano et al. [2006]. During snowfall scattering effects cause a brightness temperature enhancement for ground-based observation because the warm surface emission is scattered back towards the ground [Kneifel et al., 2010].
the solid angle. The scattering term of the radiative transfer equation needs to be used for precipitation remote sensing, e.g. Marzano et al. [2006]. During snowfall scattering effects cause a brightness temperature enhancement for ground-based observation because the warm surface emission is scattered back towards the ground [Kneifel et al., 2010].
The simulation of 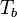 is used for the following: (a) in evaluation of forward models, in which the relevant meteorological variables are measured by radiosonde in situ soundings, (b) in inverse problems and parameter retrieval applications (see below), in which meteorological information is inferred from measurements of
is used for the following: (a) in evaluation of forward models, in which the relevant meteorological variables are measured by radiosonde in situ soundings, (b) in inverse problems and parameter retrieval applications (see below), in which meteorological information is inferred from measurements of 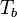 and (c) in system modeling studies, e.g. for determining the effects of instrument noise on parameter retrieval or for determining optimal measurement ordinates, such as
and (c) in system modeling studies, e.g. for determining the effects of instrument noise on parameter retrieval or for determining optimal measurement ordinates, such as 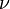 and
and 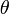 . For forward modeling the knowledge on the atmospheric absorption characteristics is fundamental (see below).
. For forward modeling the knowledge on the atmospheric absorption characteristics is fundamental (see below).
2 Microwave absorption and emission of the troposphere
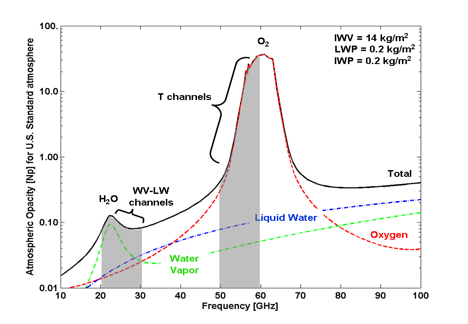
The principal sources of atmospheric microwave emission and absorption are water vapor, oxygen, and cloud liquid (Fig. 1). In the frequency region from 20 to 100 GHz, water-vapor absorption arises from the weak electric dipole rotational transition at 22.235 GHz and the so-called continuum absorption of water vapor most likely to arise from the far wing contributions of higher-frequency resonances that extend into the infrared region. It should be noted that a much stronger water vapour line exists at 183.31 GHz that is used at dry conditions [Cimini et al., 2009]. Oxygen absorbs due to a series of magnetic dipole transitions centered around 60 GHz and the isolated line at 118.75 GHz. Because of pressure broadening, i.e. the effect of molecular collisions on radiative transitions, both water vapor and oxygen absorption extend outside of the immediate frequency region of their resonant lines. There are also resonances by ozone that are important for stratospheric sounding [Klein and Gasiewski, 2000]. In addition to gaseous absorption, scattering, absorption, and emission also originate from hydrometeors in the atmosphere
Figure 1: Atmospheric opacity for U.S. standard atmosphere with liquid and ice water clouds. The ice water contribution is below 0.01 Np throughout the 10-100 GHz range. The spectral range of commercially available water vapor (WV; K-band 20-30 GHz) and temperature (V-band 50-60 GHz) microwave profilers is indicated.
2.1 Gaseous absorption models
Detailed calculations of absorption by water vapor and oxygen were first published by J. H. Van Vleck [1947a, 1947b]). The quantum mechanical basis of these calculations, including the Van Vleck-Weisskopf line shape [1947], together with laboratory measurements, has led to increasingly accurate calculations of gaseous absorption. Currently, there are several absorption models that are widely used in the propagation and remote-sensing communities. Starting with laboratory measurements that were made in the late 1960s and continuing for several years, H. Liebe developed and distributed the computer code of his Microwave Propagation Model (MPM). One version of the model [Liebe and Layton, 1987] is still used extensively and many subsequent models are compared with this one. Liebe later made changes to both water-vapor and oxygen models, especially to parameters describing the 22.235 GHz water vapor line line and the continuum [Liebe et al., 1993].
More recently, Rosenkranz [1998, 1999] developed an improved absorption model that also is extensively used in the microwave propagation community. However, there are many issues in the determination of parameters that enter into water vapor absorption modeling, and a clear discussion of several of these issues is given in Rosenkranz [1993]. Relevant to the discussion is the choice of parameters to calculate the pressure-broadened line width, which in the case of water vapor, is due to collisions of H2O with other H2O molecules (self broadening), or from collisions of H2O molecules with those of dry air (foreign broadening). In fact, Rosenkranz [1998] based his model on Liebe and Layton’s [1987] values for the foreign-broadened component, and those from Liebe et al. [1993] for the self-broadened component. A RTE model that is used extensively in the US climate research community is the Line by Line Radiative Transfer Model (LBLRTM) by S. Clough and his colleagues [Turner et al., 2003; Clough et al., 2005]. An extension of the model, called MONORTM, is most appropriate for millimeter wave and microwave radiative transfer studies [Clough et al., 2005]. MONORTM has been compared extensively with simultaneous radiation and radiosonde observations near 20 and 30 GHz. Recently, some important refinements of absorption models have occurred. In 2003 Rosenkranz refined of his 1998 code. Also Liljegren et al. [2005] incorporates the line width parameters of the 22.235 GHz model from the HITRAN data base [Rothman et al., 2005] with a different continuum formalization. Both of these new models show improvements with respect to radiative transfer modelling from clear sky radiosonde data [Mattioli et al., 2005]. In a similar appraoch Turner et al. [2009] used long-term observations in the 150 GHz window to derive an improved description for the water vapur continuum.
2.2 Extinction due to hydrometeors
For spherical particles, the classical method to calculate scattering and absorption (=extinction) is through the Lorenz-Mie Equations [Van de Hulst, 1981; Deirmendjian, 1969; Bohren and Huffman, 1983]. When calculating absorption for non-precipitating clouds the Rayleigh approximation is used, for which the liquid absorption depends only on the total liquid amount and does not depend on the drop size distribution and scattering is negligible. The Rayleigh approximation is valid when the scattering parameter 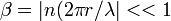 [Deirmendjian, 1969]. Here,
[Deirmendjian, 1969]. Here,  is the particle radius,
is the particle radius, 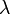 is the wavelength, and
is the wavelength, and 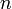 is the complex refractive index.
is the complex refractive index.
An important physical property for the calculations is the complex dielectric constant of the particle. This dielectric constant of liquid water is described by the dielectric relaxation spectra of Debye [1929]. The strong temperature dependence of the relaxation frequency is linked to the temperature dependent viscosity of liquid water. Therefore the cloud absorption coefficient also shows significant temperature sensitivity. Above 0 °C the dielectric constant can be well measured in the laboratory and a variety of measurements have been made from 5 to 500 GHz [Liebe et al., 1991]. However for super-cooled water below 0 °C, the situation is less certain and models of [Ellison, 2006; Liebe, 1991; Ray, 1972] differ by 20 to 30% in this region. This is relevant for cloud remote sensing, because measurements of super-cooled liquid are important for detection of aircraft icing [Rasmussen et al., 1992]. Recently, Mätzler et al. [2010] could show best agreement of ground-based microwave observations with a model published by Stogryn [1995]. The dielectric properties of ice [Hufford, 1991; Mätzler, 1998] are very different from those of liquid water. The dielectric losses of ice have a minimum near 1 GHz, and ice is an almost perfectly loss-free medium over a large frequency range. Therefore microwave emission of pure ice particles can be neglected in most cloud situations.
For rain and other situations for which the 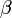 is greater than roughly 0.1, the full Mie equations, combined with a modeled (or measured) size distribution, must be used. Generally for a given wavelength and particle, the single particle contribution is calculated and the total extinction are then obtained by integration over the size distribution of particles. Due to the nonspherical shape of ice hydrometeors, the situation is more complicated when scattering plays a role. For larger snow particles scattering becomes significant at frequencies above 60 GHz and realistic models of the snow particle shape together with techniques like the Discrete Dipole Approximation need to be used to calculate the scattering properties [Kneifel et al., 2010]. Special situations occur when ice particles start to melt. A very thin skin of liquid water can be sufficient to cause significant absorption and thus emission. Usually, these conditions apply to precipitating clouds in the so-called radar "bright band".
is greater than roughly 0.1, the full Mie equations, combined with a modeled (or measured) size distribution, must be used. Generally for a given wavelength and particle, the single particle contribution is calculated and the total extinction are then obtained by integration over the size distribution of particles. Due to the nonspherical shape of ice hydrometeors, the situation is more complicated when scattering plays a role. For larger snow particles scattering becomes significant at frequencies above 60 GHz and realistic models of the snow particle shape together with techniques like the Discrete Dipole Approximation need to be used to calculate the scattering properties [Kneifel et al., 2010]. Special situations occur when ice particles start to melt. A very thin skin of liquid water can be sufficient to cause significant absorption and thus emission. Usually, these conditions apply to precipitating clouds in the so-called radar "bright band".
3 Fundamentals of radiometric systems
MWRs passively measure the natural radiation that is emitted and scattered by the atmospheric gases and hydrometeors. The measurements are sequentially or synchronously taken a several frequency channels. MWRs are usually total power instruments, i.e. they measure the signal power that is received via the antenna pattern , within the channel bandwidth and over the integration time. In order to derive profile information of humidity and temperature most channels are located along absorption features of water vapor and oxygen. In combination with an atmospheric window channel, the column integrated water vapor (IWV) and liquid water (LWP) can be retrieved from MWR measurements.
3.1 Calibration
MWR receivers provide a detector voltage which is directly related to the signal power.
In microwave radiometry, the signal power is usually expressed as a brightness temperature .
The relation between the radiometric measurement and the physical quantity is expressed by a set of parameters which are determined by the radiometer calibration.
During the calibration procedure the receivers observed at least two well-known targets, which ideally cover a large temperature range (2-point (hot/cold) calibration).
A black body target cooled by liquid nitrogen is commonly used as a cold calibration point (Liquid Nitrogen (LN2) Calibration).
The warm calibration point is provided by a black body target which is heated or is at ambient temperature ).
An advanced calibration method is the 4-point calibration which uses additional noise from an internal noise diode.
The noise is injected during the calibration process to generate to additional calibration points.
The four calibration points (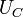 ,
, 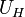 ,
, 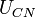 ,
, 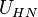 ) are then used to determine four calibration parameters being the detector gain g, the receiver noise temperature, the receiver non-linearity α and the noise diode temperature
) are then used to determine four calibration parameters being the detector gain g, the receiver noise temperature, the receiver non-linearity α and the noise diode temperature 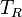 (Fig. 2).
(Fig. 2).
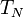 can be used as a secondary calibration standard during MWR operations.
Additionally, can serve as a reference to compensate for receiver gain drifts (hot load calibration).
can be used as a secondary calibration standard during MWR operations.
Additionally, can serve as a reference to compensate for receiver gain drifts (hot load calibration).
Alternatively to the usage of LN2, the cold calibration point can be provided by a tipping curve calibration [Han and Westwater, 2000].
This technique uses observations at different elevation angles 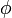 .
It is applicable to semi-transparent MWR channels. For mid-latitude close to sea level conditions the technique can be applied to K-band channels .
The technique is based on the linear relation between the air mass (approx.
.
It is applicable to semi-transparent MWR channels. For mid-latitude close to sea level conditions the technique can be applied to K-band channels .
The technique is based on the linear relation between the air mass (approx. 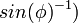 and the atmospheric opacity under horizontally homogeneous conditions.
and the atmospheric opacity under horizontally homogeneous conditions.
4 Inverse problem
Passive microwave radiometry offers the potential for retrieving the atmospheric thermodynamic state (Westwater et al. 1997), i.e. the distribution of temperature, humidity and liquid water in a quasi continuous and instantaneous way. This requires a retrieval model, which transforms the measured radiative quantities into thermodynamic information. Techniques to derive meteorological information from radiation measurements are generally based on the RTE. Because only a finite number of imperfect radiation measurements are available, and a continuum of parameters is needed to describe the thermodynamic state of the atmosphere, a rigorous mathematical solution does not exist and the inverse problem is said to be ill-posed [Twomey, 1977; Tikhonov and Arsenin, 1977]. Therefore, it is better to regard the measurements as constraints and to blend them with supplementary sources of information or to drastically reduce the dimensionality of the inverse problem by projecting the profiles onto their linear functionals. Useful supplementary information can be provided by numerical meteorological forecasts or by a priori information obtained from past data (i.e. radiosonde ascents).
4.1 Weighting functions of retrievable parameters
The information contained in ground-based MWR measurements with respect to specific atmospheric parameters can be illustrated by the concept of weighting functions. The RTE describes the radiometric response to a given atmospheric temperature 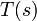 and absorption coefficient
and absorption coefficient 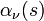 as a function of the path coordinate
as a function of the path coordinate  . The absorption coefficient, in turn, is a function of
. The absorption coefficient, in turn, is a function of 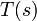 , pressure
, pressure 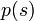 , water vapor density
, water vapor density 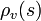 and cloud liquid density
and cloud liquid density 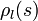 . In general, the response of
. In general, the response of 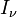 to changes of in the vertical profile of these parameters is non-linear. In order to quantify this sensitivity we can rewrite the RTE equation from above as
to changes of in the vertical profile of these parameters is non-linear. In order to quantify this sensitivity we can rewrite the RTE equation from above as
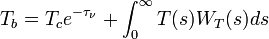
with
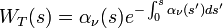
This temperature weighting functions 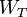 can be explicitly calculated as a function of
can be explicitly calculated as a function of 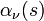 . For simplicity in notation, we have suppressed the frequency dependence of
. For simplicity in notation, we have suppressed the frequency dependence of 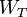 . In the direct vicinity of an absorption line the RTE can be re-written as:
. In the direct vicinity of an absorption line the RTE can be re-written as:
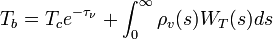
with
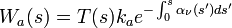
where 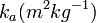 is the mass-specific absorption coefficient of the relevant absorber. Note that the term
is the mass-specific absorption coefficient of the relevant absorber. Note that the term
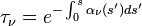
denotes the atmospheric transmission from 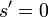 to
to 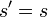 .
.
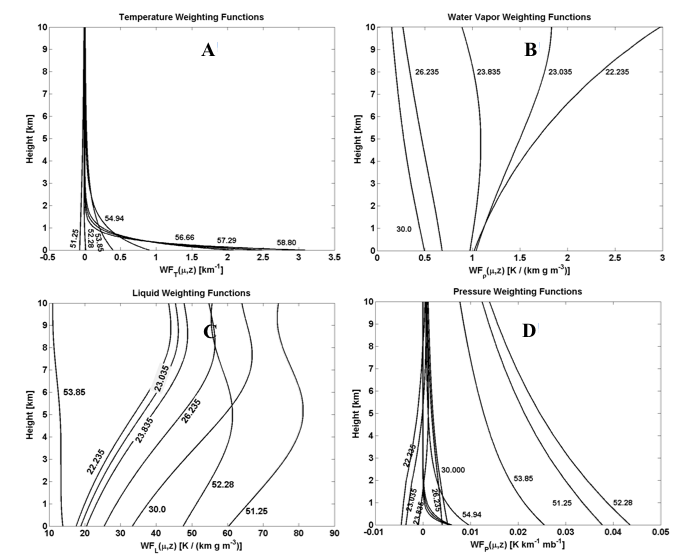
Figure 2: Weighting functions for typical profiling radiometers. A: Temperature weighting functions and center frequencies for V-band channels. High sensitivity to boundary layer temperatures is shown. B: Vapor density weighting functions and center frequencies for K-band channels. C: Liquid density weighting functions for selected channels. D: Pressure weighting functions for K- and V-band channels.
Channels in the centre of the 60 GHz oxygen absorption band are highly opaque and therefore the temperature weighting functions are strong close to the ground, i.e. the observed 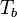 is close to the environmental temperature (Figure 2A). For frequencies further away from the centre the atmosphere is less opaque and the signal systematically stems from higher atmospheric layers. The spectral absorption features of oxygen in the microwave region allow for retrieving information on the vertical structure of temperature. The homogeneous mixing of oxygen within the troposphere results in the fact that changes of the corresponding line shapes can solely be attributed to the vertical temperature structure.
is close to the environmental temperature (Figure 2A). For frequencies further away from the centre the atmosphere is less opaque and the signal systematically stems from higher atmospheric layers. The spectral absorption features of oxygen in the microwave region allow for retrieving information on the vertical structure of temperature. The homogeneous mixing of oxygen within the troposphere results in the fact that changes of the corresponding line shapes can solely be attributed to the vertical temperature structure.
Humidity profilers typically contain channels along the 22.235 GHz line (Figure 2B). Note that the 22.235 and 23.035 GHz water vapor weighting functions increase with height, while the 23.835 GHz function is almost constant with height. Note that the vertical resolution of a typical microwave profiler in a stand-alone operation mode for humidity is very limited.
However, the constant response with height of the weighting function at 23.835 GHz implies that the channel is the most appropriate to derive Integrated Water Vapor (IWV) – the total amount of water vapor in a column of unit cross section (Westwater 1978, Hogg et al. 1983). Further discussion on the calculation of weighting functions and their significance can be found in [Westwater, 1993].
All frequencies are also strongly affected by cloud liquid water. A dual-frequency MWR using suited frequencies between 20 and 30 GHz is generally well suited for deriving the path Liquid Water Path LWP (Löhnert and Crewell, 2003). In general, multiple frequency combinations can be used to retrieve LWP and IWV due to the nearly quadratic increase of liquid water absorption with frequency. However, Löhnert and Crewell (2001) have suggested that LWP retrievals can be improved by adding a temperature-dependent frequency around 50 GHz and/or an additional frequency much more sensitive to cloud liquid water at 90 GHz. Crewell et al. [2009] could show that multi-frequency microwave radiometer measurements do not contain sufficient information to derive the liquid water content profile. However, such measurements supplemented with additional measurements of cloud base and top from active sensors such as radar and lidar can be used for profiling cloud microphysical properties.
4.2 Retrieval methodology
Existing retrievals are often categorized into statistical and “physical” algorithms. Purely statistical algorithms are based on a data set of concurrent TB and atmospheric variables, which are related to each other by means of a multi-linear regression or a neural network. The classical “physical” algorithm finds a solution such that for each case the measured brightness temperatures are sufficiently close to the ones simulated from the retrieved atmospheric state. Since a large number of atmospheric states can satisfy each combination of TBs, constraints have to be chosen, which will reduce the degrees of freedom. These constraints can be either of physical or statistical character – many retrievals apply a combination of both. One can regard the measurements as constraints and blend them with supplementary sources of information. Useful supplementary information can be provided by numerical meteorological models or by prior information obtained from past data (i.e. climatology).
Within the inversion procedure, one needs to determine the atmospheric state 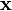 given the measurements
given the measurements 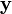 . Often in remote sensing, determining
. Often in remote sensing, determining 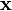 from
from 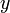 is an underdetermined and ill-conditioned problem, meaning that no unique solution exists and that very small errors in the measurement will lead to huge errors in the atmospheric profile. A way to solve this problem is to combine the measurements with a priori information, i.e. information about the atmospheric state, which is given prior to the measurement. The optimal estimation equations (e.g. Rodgers 2000) are suited for combining measurements and a priori information. An optimal atmospheric state
is an underdetermined and ill-conditioned problem, meaning that no unique solution exists and that very small errors in the measurement will lead to huge errors in the atmospheric profile. A way to solve this problem is to combine the measurements with a priori information, i.e. information about the atmospheric state, which is given prior to the measurement. The optimal estimation equations (e.g. Rodgers 2000) are suited for combining measurements and a priori information. An optimal atmospheric state 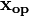 can be found by iterating the following formulation
can be found by iterating the following formulation
![\mathbf{x}_{i+1}=\mathbf{x}_{i}(\mathbf{K}_i^T\mathbf{S}_e^{-1}\mathbf{K}_i+\mathbf{S}_{ap}^{-1})^{-1}[\mathbf{K}_i^T\mathbf{S}_e^{-1}(\mathbf{y}_i-\mathbf{y})+\mathbf{S}_{ap}^{-1}(\mathbf{x}_i-\mathbf{x}_{ap})]](/wiki.eg-climet.org/images/math/9/7/8/978e3125d0b9a2e5f786d9dd319f3f4c.png)
where 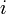 represents the iteration step,
represents the iteration step, 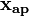 the a priori profiles (e.g. temperature, humidity and cloud properties),
the a priori profiles (e.g. temperature, humidity and cloud properties), 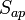 the a priori covariance matrix and
the a priori covariance matrix and 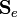 the combined measurement and forward model error covariance matrix.
the combined measurement and forward model error covariance matrix. 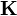 represents the so-called Jacobian, or the sensitivity of the forward model to changes in
represents the so-called Jacobian, or the sensitivity of the forward model to changes in 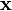 , whereby
, whereby 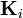 is re-calculated for each iteration. Optimally, the equation above should guarantee the minimization of a quadratic cost function between
is re-calculated for each iteration. Optimally, the equation above should guarantee the minimization of a quadratic cost function between 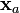 and
and 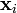 , respectively
, respectively 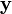 and
and 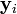 , when the difference between
, when the difference between 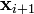 and
and 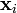 goes towards zero. It is important to note that the solution
goes towards zero. It is important to note that the solution 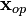 must be interpreted as the most probable solution of a Gaussian distributed probability density function, whose covariance can be written as:
must be interpreted as the most probable solution of a Gaussian distributed probability density function, whose covariance can be written as:
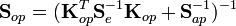
The diagonal elements of this matrix give an estimate of the mean quadratic error of 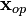 , whereas the off-diagonal elements yield information on the correlation of retrieval errors between the different heights. Such methods have been presented by Hewison et al. 2007, Cimini et al. 2012 for retrieving the vertical structure of temperature and humidity using microwave radiometry. The method has also be used to combine multiple measurements with passive microwave measurements, such as active radar and lidar remote sensors as well as optical or infrared wavelengths or even in-situ measurements (Löhnert et al. 2004, 2007, 2009).
, whereas the off-diagonal elements yield information on the correlation of retrieval errors between the different heights. Such methods have been presented by Hewison et al. 2007, Cimini et al. 2012 for retrieving the vertical structure of temperature and humidity using microwave radiometry. The method has also be used to combine multiple measurements with passive microwave measurements, such as active radar and lidar remote sensors as well as optical or infrared wavelengths or even in-situ measurements (Löhnert et al. 2004, 2007, 2009).
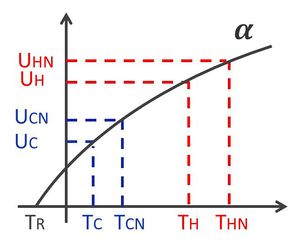
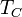 and
and 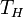 are known quantities.
are known quantities. 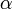 gives the non-linearity of the receiver.
gives the non-linearity of the receiver.