Raman LIDAR Fundamentals
Contents |
1 Introduction
In the following a very brief summary of the Raman lidar technique is given. In particular, temperature correction terms have been systemmatically omitted. For a detailed discussion the reader is referred to D. Whiteman, 2003a and D. Whiteman, 2003b and references therein. The rotational Raman technique to measure atmospheric temperature is discussed in more detail in Vaughan et al., 1993.
2 The LIDAR Equation
The lidar (Light Detection and Ranging) technique uses the scattering properties of molecules, aerosols and hydrometeors to derive information on the atmospheric composition or thermodynamic state. A lidar consists of a laser source, generating light pulses at a specific wavelength, of a transceiver to modify the beam diameter and divergence, and of a receiver unit (telescope, spectrometer, acquisition system), to detect the backscattered light as a function of wavelength. In the case of a Rayleigh-Mie lidar system and assuming no multiple scattering, the portion of the emitted power that is backscattered and detected by the receiver unit, 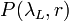 , as a function of range,
, as a function of range,  , is given by the lidar equation:
, is given by the lidar equation:
![P(\lambda_L,r) = P_0(\lambda_L) O(r) \frac{A}{r^2} C(\lambda_L,r) (\beta_{mol}(\lambda_L,r) + \beta_{aer}(\lambda_L,r)) \exp\left[-2 \int_0^r \alpha(\lambda_L,r') dr' \right] + P_{bg}](/wiki.eg-climet.org/images/math/1/e/8/1e85f661935512a0c0b67a34274ac910.png) .
.
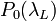 is the emitted power at laser wavelength
is the emitted power at laser wavelength 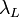 ,
, 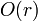 is the overlap function,
is the overlap function, 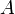 is the area of the telescope,
is the area of the telescope, 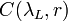 is a system constant accounting for the transmission of the receiver unit,
is a system constant accounting for the transmission of the receiver unit, 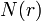 is the number density of air,
is the number density of air, 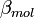 and
and 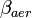 are the backscatter coefficients of air molecules and aerosols, respectively,
are the backscatter coefficients of air molecules and aerosols, respectively, 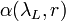 is the extinction coefficient, and
is the extinction coefficient, and 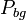 is the background power (straylight or detector noise).
is the background power (straylight or detector noise).
In the case of a Raman lidar system (inelastic scattering) the backscattered power at wavelength 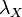 , that has been shifted from the laser wavelength due to inelastic Raman scattering by molecular species
, that has been shifted from the laser wavelength due to inelastic Raman scattering by molecular species 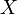 , is given by the following expression:
, is given by the following expression:
![P(\lambda_X,r) = P_0(\lambda_L) O(r) \frac{A}{r^2} C(\lambda_X,r) \beta(\lambda_L,\lambda_X,r) \exp\left[- \int_0^r \alpha(\lambda_L,r') + \alpha(\lambda_X,r') dr' \right] + P_{bg}](/wiki.eg-climet.org/images/math/e/e/5/ee5dd725940e26e8fa87c04a843bfc8c.png) .
.
The molecular backscatter coefficient is given by the number density of the scattering medium, 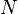 , and by the backscattering cross section
, and by the backscattering cross section 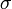 as follows:
as follows:
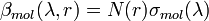 .
.
3 Raman Scattering
For inelastic scattering, the scattering molecule changes its vibrational and/or rotational energy state and hence changes the wavelength of the scattered photon. The change in wavelength depends on the two involved energy levels and is specific for the scattering molecule.
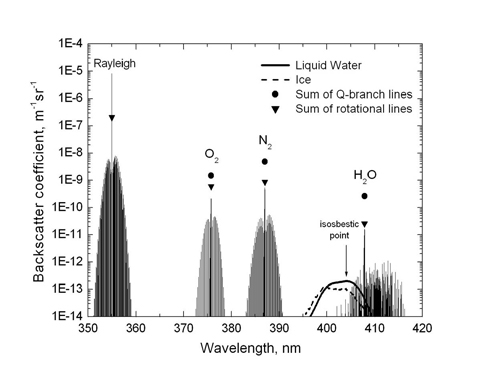
Since the population of the energy states follows a Boltzman distribution, the Raman backscatter coefficient depends on temperature. This is illustrated in the figure below.
4 Water Vapor Retrieval
For observations of water vapor, the Raman signal of water vapor at wavelength 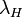 and of nitrogen at wavelength
and of nitrogen at wavelength 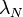 is measured. Typical wavelength pairs are
is measured. Typical wavelength pairs are 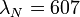 nm and
nm and 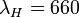 nm for stimulation at 532 nm and
nm for stimulation at 532 nm and 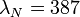 nm and
nm and 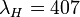 nm for stimulation at 355 nm. Using the Raman lidar equation presented above, the water vapor mixing ratio
nm for stimulation at 355 nm. Using the Raman lidar equation presented above, the water vapor mixing ratio 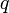 (mass of water vapor to mass of dry air) can be expressed as follows:
(mass of water vapor to mass of dry air) can be expressed as follows:
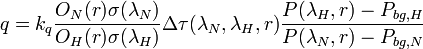
where
![\Delta\tau(\lambda_N,\lambda_H,r) = \exp\left[-\int_0^r (\alpha(\lambda_H,r') - \alpha(\lambda_N,r)) dr' \right]](/wiki.eg-climet.org/images/math/9/7/d/97d127d333101cf16e7d5c4a0e64bd68.png) .
.
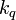 is the calibration constant and is determined based on a comparison with an external measurement like a radiosonde.
is the calibration constant and is determined based on a comparison with an external measurement like a radiosonde.
5 Aerosol Retrieval
A typical parameter that can be derived from a combined elastic-Raman lidar is the backscattering ratio 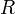 . It is defined as the ratio between the total backscatter coefficient,
. It is defined as the ratio between the total backscatter coefficient, 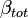 , and the molecular backscatter coefficient,
, and the molecular backscatter coefficient, 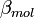 :
:
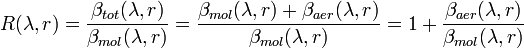 .
.
The backscattering ratio can be derived from the elastic and the Raman lidar equations and is given by:
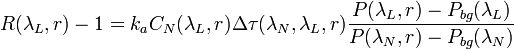 .
.
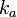 is a calibration constant and
is a calibration constant and 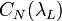 accounts for the difference in the backscatter coefficients between wavelength
accounts for the difference in the backscatter coefficients between wavelength 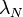 and the laser wavelength
and the laser wavelength 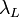 . The aerosol backscatter coefficient can be directly derived from the backscattering ratio using a molecular backscatter coefficient profile calculated from a air number density profile obtained from a radiosounding or an atmospheric model.
. The aerosol backscatter coefficient can be directly derived from the backscattering ratio using a molecular backscatter coefficient profile calculated from a air number density profile obtained from a radiosounding or an atmospheric model.
6 Temperature Retrieval
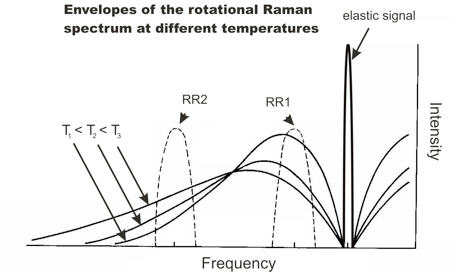
The temperature dependence of the rotational Raman spectrum is illustrated in Figure 2. Backscatter signals are measured at two different wavelengths in the rotational Raman spectrum and the temperature can be estimated from the ratio of these two signals as follows:
![T(r) = \frac{A}{\log \left[ \frac{P(\lambda_{RR1},r)-P_{bg,RR1}}{P(\lambda_{RR2},r)-P_{bg,RR2}} \right] +B}](/wiki.eg-climet.org/images/math/2/9/d/29d9a5535077e1cac72ab62f05911da0.png) .
.
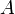 and
and 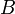 are calibration constants, that are derived from intercomparisons external measurements, typically a radiosonde.
are calibration constants, that are derived from intercomparisons external measurements, typically a radiosonde.