Signal detection, classification and moment estimation
1 Noise level estimation
To discriminate between electronic noise and echo signals, a mean noise level 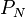 is objectively
estimated using the method of
Hildebrand and Sekhon (1974). This
method works well if white noise occupies a sufficient part of the spectrum.
is objectively
estimated using the method of
Hildebrand and Sekhon (1974). This
method works well if white noise occupies a sufficient part of the spectrum.
2 Signal peak identification
Next, the signal peak caused by the atmospheric return is selected. A simple but well-established method is to select the maximum energy peak May and Strauch (1989). The method works quite well for single peak spectra and it is called a single-peak algorithm.
Stationary clutter components will give rise to additional signal peaks. Such a situation is not accounted for in standard processing, and a variety of so-called multi-peak algorithms have therefore been proposed. Among them are simple methods, like the ground clutter algorithm by Riddle and Angevine (1991) which is in widespread use, as well as other, more complex techniques, like Griesser (1998), Cornman et.al. (1998), Law et.al. (2002), Morse et.al. (2002), or Hooper et.al. (2008).
The number of existing algorithms is symptomatic for the many different approaches to tackle the multiple peak problem. Unfortunately, there are only few validation attempts: Cohn et.al. (2001), Gaffard et. al. (2006), Hooper et.al. (2008).
The operational experience is still indicative of problems with these methods. The most important issue is the excessive use of weakly justified a-priori assumptions, like vertical continuity constraints, for peak selection. More work is needed to refine multi-peak processing.
3 Estimation of first three moments
Often the power spectrum of the atmospheric signal is assumed to have a Gaussian form though this can be violated for some radar returns, see Woodman (1985). This has the advantage that the first three moments, namely power, mean frequency and frequency spread, are sufficient for a complete description of the signal Woodman and Guillen (1974). The moments are well-defined even if the Gaussian assumption of the form of the power spectrum is violated
Echo power 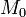 , Doppler frequency
, Doppler frequency 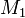 and
spectral variance
and
spectral variance  are calculated for frequency bins where
are calculated for frequency bins where ![P[i] > P_N](/wiki.eg-climet.org/images/math/9/d/a/9da0f793e61f991ce6a23163838d04d8.png) , that is between
lower and upper signal bounds
, that is between
lower and upper signal bounds 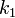 and
and 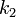 as:
as:
![M_0 = \sum_{k=k_1}^{k_2} (P[k] - P_N)](/wiki.eg-climet.org/images/math/5/d/c/5dc028732abb03888484e1790dd97e3a.png)
![M_1 = \frac{1}{M_0} \sum_{k=k_1}^{k_2} k (P[k] - P_N)](/wiki.eg-climet.org/images/math/3/e/8/3e8353a36f35c22137280a13e5cb0d85.png)
![M_2 = \frac{1}{M_0} \sum_{k=k_1}^{k_2} (k-M_1)^2 (P[k] - P_N)](/wiki.eg-climet.org/images/math/3/0/8/308ea6367a7df0f93ea767878dc51868.png)
Note that there are differences in the definitions of the spectral width. Often, the convention of
\citet{Carter_etal:95} is used, where spectral width is defined as $\sigma_v = 2 \sqrt{M_2}$.
Back to RWP Fundamentals