MWR Error characteristics
Contents |
1 Hardware
1.1 System noise
All components of a receiver system with temperatures 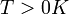 produce noise.
Besides the thermal (Nyquist) noise, there are additional contributions to the total receiver noise temperature
produce noise.
Besides the thermal (Nyquist) noise, there are additional contributions to the total receiver noise temperature 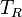 which originate from the active receiver components, like amplifiers and mixers.
The total system noise is the sum of the receiver noise and the signal noise.
which originate from the active receiver components, like amplifiers and mixers.
The total system noise is the sum of the receiver noise and the signal noise.
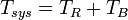
where 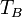 is the signal from the scene.
is the signal from the scene.
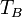 can be discriminated from the receiver noise
can be discriminated from the receiver noise 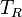 by the MWR calibration.
After Friis formula the receiver noise is composed of contributions by the different stages of the receiver chain:
by the MWR calibration.
After Friis formula the receiver noise is composed of contributions by the different stages of the receiver chain:
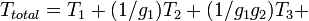 ...
...
where 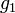 ,
, 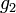 , … are the gains of each stage.
The radiometer formula describes the radiometric sensitivity
, … are the gains of each stage.
The radiometer formula describes the radiometric sensitivity
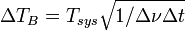
with the channels band width 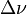 and the integration time
and the integration time 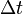 .
On the one hand, the sensitivity can be improved by increasing
.
On the one hand, the sensitivity can be improved by increasing 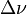 and/or
and/or 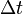 .
On the other hand, the sensitivity is proportional to the total system noise temperature
.
On the other hand, the sensitivity is proportional to the total system noise temperature 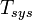 .
Consequently, reducing the receiver noise
.
Consequently, reducing the receiver noise 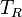 improves the signal-to-noise-ratio and the radiometric sensitivity.
For state-of the-art MWRs the receiver noise has been reduced to typical values of ~300 Kelvin in the K-band (20-30 GHz), ~350 Kelvin in the V-band (50-60GHz), ~600 Kelvin in the W-band (90GHz) and ~1200 Kelvin the G-band (183 GHz).
Assuming an integration time of 1 second and a bandwidth of 100 MHz these noise temperatures provide a measurement sensitivity which is well is below 1 Kelvin.
At the same time, the range of
improves the signal-to-noise-ratio and the radiometric sensitivity.
For state-of the-art MWRs the receiver noise has been reduced to typical values of ~300 Kelvin in the K-band (20-30 GHz), ~350 Kelvin in the V-band (50-60GHz), ~600 Kelvin in the W-band (90GHz) and ~1200 Kelvin the G-band (183 GHz).
Assuming an integration time of 1 second and a bandwidth of 100 MHz these noise temperatures provide a measurement sensitivity which is well is below 1 Kelvin.
At the same time, the range of 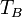 is still small in comparison with
is still small in comparison with 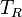 .
This means that the impact of the receiver non-linearities is also small (see Sect. Calibration Uncertainties).
.
This means that the impact of the receiver non-linearities is also small (see Sect. Calibration Uncertainties).
1.2 Calibration uncertainty
The calibration uncertainties are discussed for two calibration techniques, which are widely used for MWRs.
The uncertainties are mostly related to uncertainties at the calibration points.
Generally, these uncertainties mostly affect observations in the vicinity of the particular calibration point.
An exception is the detector non-linearity, which has the largest impact on measurement between the cold and the hot calibration point.
However, the non-linearity can be considered by the calibration parameter α.
In case 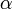 is not considered the calibration uncertainty may be reduced by a few tenth of a Kelvin.
In the same order is the uncertainty which arises from the uncertainty
The uncertainty at the ambient/hot calibration point, which arises from the in-situ temperature measurement of the target, is in the same order.
However, the main contribution to the calibration accuracy results from uncertainties at the cold calibration point.
is not considered the calibration uncertainty may be reduced by a few tenth of a Kelvin.
In the same order is the uncertainty which arises from the uncertainty
The uncertainty at the ambient/hot calibration point, which arises from the in-situ temperature measurement of the target, is in the same order.
However, the main contribution to the calibration accuracy results from uncertainties at the cold calibration point.
1.2.1 Liquid Nitrogen (LN2) Calibration
For the LN2 calibration the cold calibration point is realized by an external LN2 target The uncertainty of this calibration point mainly results from a reflective component that superimposes with the black body emission of the cooled LN2 target. The reflective component arises from a non-zero reflectivity of the LN2 surface leading to a contribution of the receiver’s thermal emission when observing the LN2 target. The reflections can only be considered within the accuracy limits of the refractive index of LN2 derived from laboratory measurements. In addition to the single-reflection, the LN2 surface favors standing waves building up the between the receiver and the surface. A smaller contribution to the calibration uncertainty arises from the in-situ temperature measurement of the ambient/hot calibration target. Even when standing waves can be excluded, the overall absolute accuracy of the LN2 calibration is assessed to be in the order of 1 Kelvin [Maschwitz et al., 2013].
1.2.2 Tipping Curve Calibration
This technique derives a cold calibration point from scene observations. It assumes that the atmosphere is horizontally homogenous. Any deviation from this assumption leads to deviating calibration results. Therefore, quality thresholds are applied to the tipping curve observations. In practice, there is still significant impact of residual atmospheric inhomogeneities in the order of several tenths of a Kelvin. Additionally, there are systematic effects which can be avoided by considering the antenna beam width and the Earth's curvature along the slant observation path. When these effects are considered, the overall absolute accuracy is in the order of 0.5 Kelvin [Maschwitz et al., 2013].
1.3 External sources
Due to the increased use of wireless communication Radio Frequency Interference (RFI) has become problematic not only at lower frequencies but even at protected frequencies, e.g., 24 GHz. RFI can cause spikes in the data. Although the modern MWR systems have implemented RFI protection measures, strong transmitters, especially in the 22 to 30 GHz and 51 to 59 GHz regions can interfere with the MWR observations. Spikes with magnitude greater than several K shall be regarded as suspected of RFI contamination. The MWR units should be installed in a location that is isolated or shielded from strong radio transmitters.
2 Retrieval
2.1 Absorption model uncertainties
Radiation absorption by atmospheric gases and hydrometeors is quantitatively modelled while solving the forward problem and thus absorption model uncertainties affect all the retrieval methods based on simulated brightness temperatures 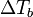 . Only retrieval methods based on historical datasets of MWR observations and simultaneous atmospheric soundings are not affected by absorption model uncertainties. The most relevant absorption features in the 20-60 GHz range come from water vapour, oxygen, and liquid water. Modifications of absorption models are continuously proposed based on laboratory data and MWR field observations (Cimini et al. 2004; Liljergren et al. 2005; Hewison et al., 2006; Clough et al. 2006; Cadeddu et al. 2007, Payne et al. 2008, Turner et al. 2009). For water vapour, the absorption model uncertainties are approximately within 5% (Payne et al. 2008, 2011), which dominate the measurement error budget especially for high-humidity conditions. For oxygen, different absorption models agree very well (0.3%) at opaque channels (56-60 GHz), but show larger differences between them and with respect to MWR observations at more transparent channels (50-56 GHz). These uncertainties are quite consistent and can be effectively mitigated with bias removal solutions. Without any intervention, absorption model uncertainties in the 50-56 GHz range may bias temperature retrievals in the upper atmosphere, but have negligible effect in the boundary layer. For liquid water, the major uncertainties are related to supercooled water, i.e. liquid water at sub-freezing temperatures, since absorption models at these temperatures is primarily based on extrapolations from higher temperature regions. Partly due to lack of laboratory measurements for liquid water at low temperatures, the mass absorption coefficients calculated by different models at 31.4 GHz deviate by about 5% at 0°C and up to 50% at −30°C (Kneifel et al. 2010), but there have been some recent advances in this area (e.g., Cadeddu and Turner 2011). Nonetheless, liquid water path measurements at sub-freezing temperatures should be interpreted with care.
. Only retrieval methods based on historical datasets of MWR observations and simultaneous atmospheric soundings are not affected by absorption model uncertainties. The most relevant absorption features in the 20-60 GHz range come from water vapour, oxygen, and liquid water. Modifications of absorption models are continuously proposed based on laboratory data and MWR field observations (Cimini et al. 2004; Liljergren et al. 2005; Hewison et al., 2006; Clough et al. 2006; Cadeddu et al. 2007, Payne et al. 2008, Turner et al. 2009). For water vapour, the absorption model uncertainties are approximately within 5% (Payne et al. 2008, 2011), which dominate the measurement error budget especially for high-humidity conditions. For oxygen, different absorption models agree very well (0.3%) at opaque channels (56-60 GHz), but show larger differences between them and with respect to MWR observations at more transparent channels (50-56 GHz). These uncertainties are quite consistent and can be effectively mitigated with bias removal solutions. Without any intervention, absorption model uncertainties in the 50-56 GHz range may bias temperature retrievals in the upper atmosphere, but have negligible effect in the boundary layer. For liquid water, the major uncertainties are related to supercooled water, i.e. liquid water at sub-freezing temperatures, since absorption models at these temperatures is primarily based on extrapolations from higher temperature regions. Partly due to lack of laboratory measurements for liquid water at low temperatures, the mass absorption coefficients calculated by different models at 31.4 GHz deviate by about 5% at 0°C and up to 50% at −30°C (Kneifel et al. 2010), but there have been some recent advances in this area (e.g., Cadeddu and Turner 2011). Nonetheless, liquid water path measurements at sub-freezing temperatures should be interpreted with care.
2.2 Information content and accuracy specification
In order to derive atmospheric profiles of temperature and humidity from radiance observations, a retrieval model, which transforms the measured radiative quantities into thermodynamic information, is needed. In general, the retrieval problem is underdetermined, implying that no unique solution of the thermodynamic structure exists in correspondence to the measurements. Rather, a wide range of possible thermodynamic structures can result in the same measured radiative quantities, so that further assumptions and additional measurements are needed to narrow down the range of valid thermodynamic solutions. The vertical resolution of a typical microwave profiler in a stand-alone operation mode for temperature and humidity retrieval is very limited (e.g., Güldner and Spänkuch, 2001). Cadeddu et al. (2002) have applied a multi-resolution wavelet transform technique for studying the vertical resolution of temperature profiles from a multi-frequency microwave profiler and found rapidly degrading values of 125 m in 400 m height to about 500 m in 1.5 km height at zenith viewing direction.
An objective way to analyze the information content of MWR retrievals is to evaluate the number of degrees of freedom (DOF) for a set of retrieved profiles; i.e. the number of independent levels of temperature or humidity that can be determined. An important measure for such an evaluation is the averaging kernel matrix 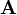 that states the sensitivity of the retrieved to the true state. In the case of Gaussian statistics,
that states the sensitivity of the retrieved to the true state. In the case of Gaussian statistics, 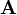 can be written as
can be written as
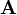 =
=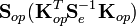
The columns of 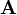 are frequently used as a measure of vertical resolution (Rodgers 2000), whereas the trace of
are frequently used as a measure of vertical resolution (Rodgers 2000), whereas the trace of 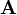 states the independent number of levels
that can be retrieved from a given measurement.
states the independent number of levels
that can be retrieved from a given measurement.
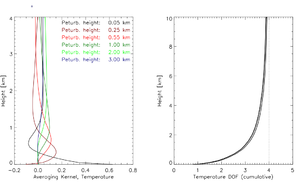
As an example Fig. 1 shows the number of independent pieces of information contained in the TB for retrieving the temperature profile using the average (1992–2009) Payerne profile of temperature,
humidity and pressure. The calculated averaging kernels for 6 distinct heights are shown. A perfect vertical resolution would give rise to a delta function with a value of 1 at height 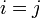 and 0 at all other heights. The broadness of the averaging kernels gives information on the vertical resolution. The total DOF are 4 in case of the temperature retrieval. If the cumulative distribution
of the DOF with height is regarded, one can conclude that about 85% (95 %) of the temperature information originates from the lowest 2 km (4 km). Further information on the accuracy of retrievals of temperature, humidity and cloud liquid water from MWR can be found in section 3 of the EG-CLIMET final report.
and 0 at all other heights. The broadness of the averaging kernels gives information on the vertical resolution. The total DOF are 4 in case of the temperature retrieval. If the cumulative distribution
of the DOF with height is regarded, one can conclude that about 85% (95 %) of the temperature information originates from the lowest 2 km (4 km). Further information on the accuracy of retrievals of temperature, humidity and cloud liquid water from MWR can be found in section 3 of the EG-CLIMET final report.
3 BIAS detection
Next to the random errors, retrievals are also almost always subject to systematic error. Such errors can originate from instrumental effects as well as from the radiative transfer simulation. However, systematic errors may be reduced through assessing the systematic 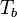 offsets. During clear sky situations MWR measurements and radiative transfer calculations using collocated radiosonde data and/or model analyses can show significant differences. Principally perfect agreement is not expected because the MWR performs a point measurement in time and captures the whole atmospheric column within an instant, while the radiosonde is subject to wind drift and has an ascent time of 30 min before reaching the top of the troposphere. However, no significant systematic error is to be expected from this discrepancy.
offsets. During clear sky situations MWR measurements and radiative transfer calculations using collocated radiosonde data and/or model analyses can show significant differences. Principally perfect agreement is not expected because the MWR performs a point measurement in time and captures the whole atmospheric column within an instant, while the radiosonde is subject to wind drift and has an ascent time of 30 min before reaching the top of the troposphere. However, no significant systematic error is to be expected from this discrepancy.
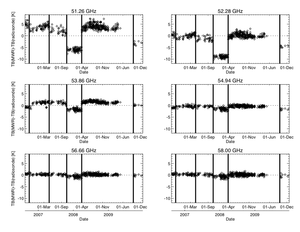
Examplarily, results of such comparisons are shown in Fig. 2, which makes clear that large systematic offsets of up to 5K and more are evident in the more transparent V-band channels. 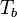 offsets are also present in the off-zenith observing directions - here the necessity of considering the offset correction for the optically thinner frequency channels even down to
low elevation angles is necessary.
offsets are also present in the off-zenith observing directions - here the necessity of considering the offset correction for the optically thinner frequency channels even down to
low elevation angles is necessary.
The fact that some of the observed offsets seem to “jump” after each LN2 calibration, hints towards a problem with the calibration. Typical error sources in the LN2 calibration procedure are water condensate forming on the aluminium plate
reflector connecting the cold load and the radiometer or on the radiometer radome itself, as well as a non-homogenous
covering of the absorber material of the cold load with LN2. 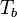 offsets after the first, second and fourth calibrations resemble each other, while the
offsets after the first, second and fourth calibrations resemble each other, while the 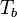 offsets after the third and fifth calibration are also similar to each other. We here assume that the third and fifth calibrations were faulty in the sense that water condensate formed on the aluminium plate or the radome leading to an additional emission signal and in consequence to a underestimation of the TBs. In order to prevent this, MWR radome blowers and heaters should be operated with maximum power and continuous checks of the radome state should be carried out during calibration. The effect of accounting for the bias correction can be seen in section 3.1.4.
offsets after the third and fifth calibration are also similar to each other. We here assume that the third and fifth calibrations were faulty in the sense that water condensate formed on the aluminium plate or the radome leading to an additional emission signal and in consequence to a underestimation of the TBs. In order to prevent this, MWR radome blowers and heaters should be operated with maximum power and continuous checks of the radome state should be carried out during calibration. The effect of accounting for the bias correction can be seen in section 3.1.4.
Clear-sky radiosonde and/or model analysis data should be also be used to quality controll 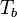 measurements in the K-band, which are mainly sensitive to water vapor. Although, water vapor is subject to rapid changes, systematic calibration offset - and thus the need to re-calibrate the instrument - can be frequently identified.
measurements in the K-band, which are mainly sensitive to water vapor. Although, water vapor is subject to rapid changes, systematic calibration offset - and thus the need to re-calibrate the instrument - can be frequently identified.
4 Quality flagging
Quality control procedures to check the quality of observed 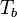 and retrieved products are fundamental for providing the users with the means for judging and eventually screening the data. A continuous data flow and data base ingestion to a central server presents the basis for an observational network aiming at near real time applications. Ideally the data flow should be based on an uninterrupted at least once a day data file transfer. Quick looks of the level1 (
and retrieved products are fundamental for providing the users with the means for judging and eventually screening the data. A continuous data flow and data base ingestion to a central server presents the basis for an observational network aiming at near real time applications. Ideally the data flow should be based on an uninterrupted at least once a day data file transfer. Quick looks of the level1 (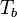 ) and level2 (IWV & LWP) data should be made automatically visible via the web.
) and level2 (IWV & LWP) data should be made automatically visible via the web.
Quality control procedures have been developed by MWR manufactures running with the acquisition software as well as by operators based on their experience. The quality control procedure may be instrument specific and/or adaptable to other instruments. Most manufacturers have installed rain sensors on their instruments that detect the presence of rain and warn the operator when the MWR may be wet and thus the TB obscured. However screening data based on rain flag only may result in “overkilling” because rain sensors may react too sensitive to increases in humidity. It is advisable to compare the rain flag with independent measurements such as webcam, rain gauge or IR camera if available.
Some manufacturer’s record quality flags of the receiver system in so-called housekeeping data files. These include the measurements of voltages and temperature at significant points within the signal processing chain and thus give information on the trustworthiness of the TB s as well as the necessity to contact the manufacturer in case of severe failure. Cases when the MWR records non-physical brightness temperatures (i.e. lower than 2.7 K or higher than a threshold values of 330 K) should also be flagged.
Quality control for atmospheric observations may be carried by analysing the 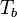 spectrum. E.g., if the spectrum reveals that the water vapour line at 22.2 GHz is obscured by the continuum emission from liquid water, then the quality of water vapor profiles is degraded accordingly. The same may apply for temperature profiles. Such a quality flag (high/medium/low) is variable-dependent – e.g. the quality of boundary layer temperature profiles stays medium even under light precipitation as slant observations and opaque channels are less affected by rain. A further criterion should also be a check if non-physical air temperatures (i.e. lower than 180 K and higher than 330 K) or humidity values are retrieved. LWP values smaller than -50
spectrum. E.g., if the spectrum reveals that the water vapour line at 22.2 GHz is obscured by the continuum emission from liquid water, then the quality of water vapor profiles is degraded accordingly. The same may apply for temperature profiles. Such a quality flag (high/medium/low) is variable-dependent – e.g. the quality of boundary layer temperature profiles stays medium even under light precipitation as slant observations and opaque channels are less affected by rain. A further criterion should also be a check if non-physical air temperatures (i.e. lower than 180 K and higher than 330 K) or humidity values are retrieved. LWP values smaller than -50 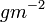 also hint towards measurement problems and further problem solving should be undertaken.
also hint towards measurement problems and further problem solving should be undertaken.
Finally, experience has shown that not all faulty measurements may be detected automatically. In order to filter suspicious cases, it is recommended to manually inspect the daily quicklooks of 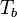 , LWP and IWV before storing the data in its final form. This “by eye” inspection will lead to confident
, LWP and IWV before storing the data in its final form. This “by eye” inspection will lead to confident 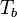 values without inconsistencies in the measurements (i.e. spikes), which may be caused by RFI or non-meteorological “disturbances” (sun, moon, humans, birds, aircraft, …). Condensation/evaporation of liquid water on the radome is characterized by a steady and regular increase/decrease of the
values without inconsistencies in the measurements (i.e. spikes), which may be caused by RFI or non-meteorological “disturbances” (sun, moon, humans, birds, aircraft, …). Condensation/evaporation of liquid water on the radome is characterized by a steady and regular increase/decrease of the 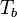 signals in the K-band and transparent V-band channels. Such behaviour it is also generally visible in the retrieved measurements of LWP and can, with some practice, be easily discriminated from a liquid cloud signal.
signals in the K-band and transparent V-band channels. Such behaviour it is also generally visible in the retrieved measurements of LWP and can, with some practice, be easily discriminated from a liquid cloud signal.