Estimation of the Doppler spectrum
1 Generalities
With the assumption that the coherently integrated time series ![S^{ci} [m]](/wiki.eg-climet.org/images/math/2/7/a/27a5cb90c5bad63b50ea46dc7fdc7fbd.png) for atmospheric
returns can be regarded as a stationary Gaussian random process, it suffices to estimate the power
spectrum for a description of this process without loss of information. The latter is usually referred
to as the Doppler spectrum.
More information on spectral estimation can be found in Percival and Walden (1993).
for atmospheric
returns can be regarded as a stationary Gaussian random process, it suffices to estimate the power
spectrum for a description of this process without loss of information. The latter is usually referred
to as the Doppler spectrum.
More information on spectral estimation can be found in Percival and Walden (1993).
2 Periodogram
In RWP processing, a modified periodogram is used as a classical
nonparametric estimator of the power spectrum. This method
needs no further a-priori information and produces reasonable results for a large class of relevant
processes, including ground clutter and some types of Radio Frequency Interference (RFI).
The (leakage) bias of the periodogram estimate is reduced through data tapering, e.g. the time series is
multiplied with a window sequence ![w[n]](/wiki.eg-climet.org/images/math/0/4/6/046349398007dbd86775d869dccf238b.png) . A Hanning window is often employed for it is
conveniently implemented in the frequency domain, but in general a variety of windows is at disposal, see
Harris (1978).
. A Hanning window is often employed for it is
conveniently implemented in the frequency domain, but in general a variety of windows is at disposal, see
Harris (1978).
For a reduction of the variance of the estimate, there are basically three options:
- The whole time series is transformed through a DFT and the estimate is smoothed across frequencies (lag window spectral estimator), see e.g. Muschinski et.al. (2005)
- The time series is broken up into
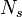 segments of equal length, the direct spectral estimate is computed for each segment and the
segments of equal length, the direct spectral estimate is computed for each segment and the 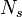 estimates are averaged together. This is called Welch's overlapped segment averaging (WOSA) estimator Welch (1967). It is popular due to its easy implementation and known as spectral or incoherent averaging in the RWP community, see e.g. Strauch et.al. (1984)
estimates are averaged together. This is called Welch's overlapped segment averaging (WOSA) estimator Welch (1967). It is popular due to its easy implementation and known as spectral or incoherent averaging in the RWP community, see e.g. Strauch et.al. (1984)
- A series of estimates is calculated using a set of orthogonal data tapers, which are then averaged together. This multitaper estimator was proposed by \citet{Thomson:82} and recently used by Anandan et.al. (2004).
3 WOSA
The WOSA approach without overlapping of the blocks is implemented as follows: For 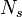 segments of length
segments of length 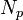 , single spectrum estimates are obtained for
, single spectrum estimates are obtained for
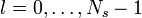 , with
, with 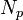 discrete frequencies,
discrete frequencies, 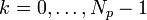 as
as
![P[l,k] = \frac{1}{N_p}\left | \sum_{m=0}^{N_p-1}w[m] {S^{ci}[l \cdot N_p + m]} e^{-i\frac{2\pi
km}{N_p}} \right |^2](/wiki.eg-climet.org/images/math/0/a/f/0af05bcae138d8869cf56e8904c97352.png) ,
,
and simple averaging then yields the estimate
![P[k] = \frac{1}{N_{s}}\sum_{l=0}^{N_{s} -1} P[l,k]](/wiki.eg-climet.org/images/math/9/7/e/97ee2001c3dea65befa2f119b41b8c44.png)
The Doppler spectrum is usually given as a function of velocity instead of frequency. The conversion
between frequency shift 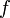 and radial velocity
and radial velocity 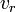 uses the well-known relation
uses the well-known relation
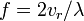 , where
, where 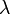 denotes the radar wavelength.
denotes the radar wavelength.
The dwell time for the estimation of a Doppler spectrum is 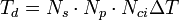 .
.
Back to RWP Fundamentals