Demodulation, range gating and A/D conversion
Contents |
1 Narrowband receiver signal
The narrow-band RWP signal at the output port of the low noise amplifier can be written as
![S_{rx}(t)=A(t)\cos \left[\omega_c t + \Phi(t)\right]](/wiki.eg-climet.org/images/math/2/3/8/238f5f1ffe28420bfc37a45802f9e6be.png) .
.
All available information about the scattering process is contained in the amplitude and phase
modulation of the received signal 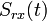 . It is technically difficult to sample such a signal,
therefore a demodulation step is performed first, which essentially removes the irrelevant carrier
frequency
. It is technically difficult to sample such a signal,
therefore a demodulation step is performed first, which essentially removes the irrelevant carrier
frequency 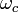 while the modulation information contained in the instantaneous amplitude
while the modulation information contained in the instantaneous amplitude 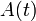 and the instantaneous phase
and the instantaneous phase 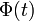 remains unchanged.
remains unchanged.
2 Demodulation: Analytic signal
For demodulation, a new signal 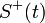 with the Fourier spectrum
with the Fourier spectrum 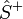 is created:
is created:
![\hat{S}^{+}(\omega) = \hat{S}(\omega) + \sgn\left[\omega\right] \hat{S}(\omega)](/wiki.eg-climet.org/images/math/0/c/0/0c0b96bd9b8bf02aef45b511b781986b.png) .
.
This operation removes the negative part of the original signal spectrum. The signal 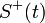 is called the analytic signal or pre-envelope of
is called the analytic signal or pre-envelope of 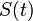 , see
McDonough and Whalen (1995) .
, see
McDonough and Whalen (1995) .
In the time domain, it is formed as
![S^{+}(t) = S(t) + i \mathcal{H}\left[S(t)\right]](/wiki.eg-climet.org/images/math/0/2/e/02e397c096d6d382fe9fc1fb50300386.png) ,
,
where the operator 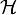 denotes the Hilbert transform.
denotes the Hilbert transform.
The analytic narrowband signal can be written as
![S^{+}(t) = \left[\tilde{S}(t)e^{i\omega_c t} \right]](/wiki.eg-climet.org/images/math/c/a/0/ca05ccc5501b5b6835586c95fbc15cec.png) ,
,
where 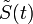 is the complex envelope of the original signal. Multiplication of
is the complex envelope of the original signal. Multiplication of 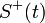 with
with
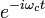 removes the carrier and gives the complex envelope
removes the carrier and gives the complex envelope
![\tilde{S}(t) = S^{+}(t) e^{-i \omega_c t} = (S(t) + i \mathcal{H}\left[S(t)\right]) e^{-i\omega_c t} = I(t) + i Q(t)](/wiki.eg-climet.org/images/math/1/1/6/1162115e1db7cb4a858a363d89e123f6.png) ,
,
where the real part of the complex envelope is the so-called in-phase 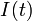 and the imaginary part
and the imaginary part
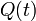 the quadrature phase of the signal. The Hilbert transform is not easily implemented in real systems.
Instead, the in-phase and quadrature-phase components are determined using a quadrature
demodulator. Details depend on the receiver architecture of the RWP.
the quadrature phase of the signal. The Hilbert transform is not easily implemented in real systems.
Instead, the in-phase and quadrature-phase components are determined using a quadrature
demodulator. Details depend on the receiver architecture of the RWP.
3 Range gating
For a fixed beam direction, RWP transmit a series of short electromagnetic pulses, each one separated by
a time interval 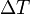 . For a single pulse, the
sampling in time allows the determination of the radial distance of the measurement using the well-known
propagation speed of the wave group. The maximum distance for unambiguously determining the measurement
distance is limited by the pulse separation or inter-pulse-period
. For a single pulse, the
sampling in time allows the determination of the radial distance of the measurement using the well-known
propagation speed of the wave group. The maximum distance for unambiguously determining the measurement
distance is limited by the pulse separation or inter-pulse-period 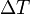 and
and  is called the maximum unambiguous range.
is called the maximum unambiguous range. 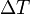 has to be set sufficiently high to prevent range
aliasing problems, that is arrival of backscattering signals from the preceding pulse after the next
pulse is transmitted. For a typical wind profiler it is if the order of
has to be set sufficiently high to prevent range
aliasing problems, that is arrival of backscattering signals from the preceding pulse after the next
pulse is transmitted. For a typical wind profiler it is if the order of 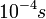 .
.
Range gating is usually done in the A/D process using sample and hold circuitry. The sample strobe
required for range gating and pulse repetition is provided by the radar controller. If the range
sampling frequency is given by 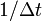 and
and 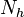 is an integer denoting the number of range gates
with
is an integer denoting the number of range gates
with 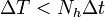 , then signal
, then signal 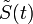 is obtained at the discrete grid
is obtained at the discrete grid
![\tilde{S}[j,n] = \tilde{S}(t_0 + j \Delta t + n \Delta T)~, j = 0,\ldots ,N_h -1,~~ n = 0, \ldots, N_T-1](/wiki.eg-climet.org/images/math/7/9/f/79f133b728a0cc35ef28b0ab73155655.png) .
.
For each range gate 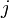 , that is for the height
, that is for the height 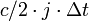 , a discrete time series of
the complex envelope of the signal with a sampling interval of
, a discrete time series of
the complex envelope of the signal with a sampling interval of 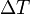 is obtained (Hardware effects like the group delay of the pulse in the radar electronics are ignored for simplicity).
is obtained (Hardware effects like the group delay of the pulse in the radar electronics are ignored for simplicity).
4 RWP raw data
For every range gate, a complex time series is obtained as
![S[n] = S_I[n] + i S_Q[n], \qquad n=0,...,N_T-1](/wiki.eg-climet.org/images/math/3/3/b/33bdd13cd99ead33369f89ed8d691255.png) .
.
Note that the range gate index and the tilde denoting the complex envelope are suppressed for convenience.
Back to RWP_Fundamentals