Cloud radar error characteristics
1 Error characteristics
Despite of the good performance of cloud radars the accuracy of reflectivity 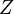 measurements may be crucial especially for the estimation of microphysical cloud parameters. The accuracy of
measurements may be crucial especially for the estimation of microphysical cloud parameters. The accuracy of 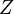 depends primarily on radar calibration and on the propagation of electromagnetic waves (Lhermitte 1990, cf. Danne 1996)in the wet atmosphere. Therefore, a well calibrated radar is a pre-assumption for the application of many retrieval techniques and for providing cloud parameters comparable between different locations. Among the calibration and attenuation issue the accuracy may be also reduced by a wet antenna and by occasional artificial signals caused by antenna sidelobes or by artificial targets (e.g. Görsdorf at al. 2012). Furthermore, there are doubts if incoherent scattering is the only scattering process as there might be contributions from coherent scattering as described in Russchenberg et al., 2009 and Argyrouli at al., 2012. Undouptedly, radar calibration is one of the main issue for accurate reflectivity measurements and will be therefore discussed in more detail.
depends primarily on radar calibration and on the propagation of electromagnetic waves (Lhermitte 1990, cf. Danne 1996)in the wet atmosphere. Therefore, a well calibrated radar is a pre-assumption for the application of many retrieval techniques and for providing cloud parameters comparable between different locations. Among the calibration and attenuation issue the accuracy may be also reduced by a wet antenna and by occasional artificial signals caused by antenna sidelobes or by artificial targets (e.g. Görsdorf at al. 2012). Furthermore, there are doubts if incoherent scattering is the only scattering process as there might be contributions from coherent scattering as described in Russchenberg et al., 2009 and Argyrouli at al., 2012. Undouptedly, radar calibration is one of the main issue for accurate reflectivity measurements and will be therefore discussed in more detail.
2 Radar calibration
The radar reflectivity 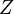 is proportional to the signal-to-noise ratio (SNR) of the received signal, whereby the proportionality factor
is proportional to the signal-to-noise ratio (SNR) of the received signal, whereby the proportionality factor 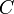 takes into account all system properties (Doviak/Zrnic:93):
takes into account all system properties (Doviak/Zrnic:93):
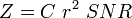
The determination of 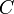 is usually denoted as radar calibration.
Radar systems can be calibrated indirectly by measurements of individual system parameters, externally using point targets or by comparison with other (reference) reflectivity profiles.
Radars with a scanning antenna can apply the external calibration by measuring the return signal from a defined reflector of known cross section. Bergada et al. (2001) describe the calibration of a 35 GHz and 94 GHz radar using triangular corner reflectors of two different sizes and metal spheres of three different sizes. Spheres proved to work better at 35 GHz band while corner reflector measurements were more stable at 94 GHz band.
Protat et al. (2011) propose a method for calibrating ground based cloud radar systems by means of the spaceborne 94 GHz cloud radar CloudSat. Beside the calibration of 94 GHz radars the technique is also applicable to 35 GHz radars. Hogan et al. (2003) describe a calibration method for 94 GHz systems which is based on the attenuation of the radar signal during rain.
is usually denoted as radar calibration.
Radar systems can be calibrated indirectly by measurements of individual system parameters, externally using point targets or by comparison with other (reference) reflectivity profiles.
Radars with a scanning antenna can apply the external calibration by measuring the return signal from a defined reflector of known cross section. Bergada et al. (2001) describe the calibration of a 35 GHz and 94 GHz radar using triangular corner reflectors of two different sizes and metal spheres of three different sizes. Spheres proved to work better at 35 GHz band while corner reflector measurements were more stable at 94 GHz band.
Protat et al. (2011) propose a method for calibrating ground based cloud radar systems by means of the spaceborne 94 GHz cloud radar CloudSat. Beside the calibration of 94 GHz radars the technique is also applicable to 35 GHz radars. Hogan et al. (2003) describe a calibration method for 94 GHz systems which is based on the attenuation of the radar signal during rain.
External methods are not ever applicable for all radar systems. For vertical pointing radars with a fixed antenna and narrow beam width (large apertures) calibration using corner relfectors is a difficult task. Therefore, the indirect method (named also as budget calibration) is still the standard for many cloud radars. A calibration study for ARM site radars MMCR can be found in Mead, 2010. Here an error estimation will be given on example of Meteks MIRA36, which were taken into operation at many sites in Europe during the last years.
The radar constant 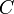 in equation above can be written as
in equation above can be written as
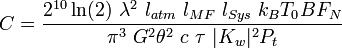
To calculate 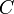 , the gain and loss are determined for each component of the radar once during manufacture. In addition the transmitting power is measured continuously and the noise figure of the receiver is monitored by an internal noise source. The following table lists all parameters and their estimated errors.
, the gain and loss are determined for each component of the radar once during manufacture. In addition the transmitting power is measured continuously and the noise figure of the receiver is monitored by an internal noise source. The following table lists all parameters and their estimated errors.
| parameter | value | error | 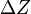
| |
|---|---|---|---|---|
| Transmitting power | 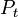 |
20..30 kW | 3.5 kW | 0.4 dB |
| Matched filter loss | 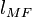 |
1.7 dB | 0.3 dB | 0.3 dB |
| Receiver Noise Figure |  |
6.0 dB | 0.5 dB | 0.5 dB |
| Loss by wave guides: antenna - receiver | 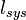 |
2*0.65*length [dB] | 0.2 dB | 0.2 dB |
| Antenna aperture | 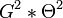 |
1.5 dBi | 1.5 dB | 1.5 dB |
| Pulse length | 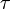 |
200 ns | ||
| Wave length | 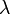 |
0.0824 m | ||
| Speed of light |  |
2.998x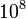 m/s m/s |
0.001x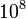 m/s m/s |
0.001 dB |
| Constant | 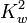 |
0.93 | 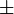 0.2 0.2 |
0.09 dB |
The antenna parameters account to the radar constant by the factor 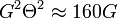 , because the gain is related to the beam width by
, because the gain is related to the beam width by 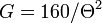 . The impact of
. The impact of  is not considered here.
is not considered here.
The maximum error of 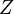 is the sum of each individual error component and amounts to about 3.0 dBz.
That is the worst case when all errors have the same direction. In reality it should be much smaller. But, nevertheless an independent check would be very valuable.
is the sum of each individual error component and amounts to about 3.0 dBz.
That is the worst case when all errors have the same direction. In reality it should be much smaller. But, nevertheless an independent check would be very valuable.
Back to Cloud radar