Lidar fundamentals
Contents |
1 Fundamentals of Lidar
The lidar profiling technique (Fiocco, 1963) is based on the study of the interaction between a laser radiation sent into the atmosphere and the atmospheric constituents. The interaction process of a dispersed medium consisting of aerosol or cloud particles suspended at random in the atmosphere can be described by the Beer-Bouguer-Lambert law as:
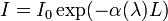
where 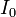 is incident light intensity,
is incident light intensity, 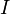 is light intensity transmitted through the medium in the forward direction (i.e. parallel to the incident light),
is light intensity transmitted through the medium in the forward direction (i.e. parallel to the incident light), 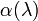 is volumetric extinction coefficient; and L is geometric distance between emitter and receiver.
The transmitted light is partially reflected or scattered back to the instrument. Radiation (photons) backscattered by the target is collected by a telescope, used as a receiver, and processed to yield information about the observed target. The processing consists of a spectral selection step, made by using a combination of optical elements, and a detection phase operated by means of different devices, such as photomultipliers or avalanche photodiodes, depending on the detected wavelength. The detectors convert the radiation in output electrical signals that, suitably processed, provide vertical profiles of the atmospheric properties as well as the concentration of atmospheric constituents.
Light scattering in the atmosphere includes a large variety of elastic and inelastic processes. The backscattered lidar signal typically consists of elastic scattering from both molecules and particles and of inelastic scattering due to rotational Raman transition in molecules. Lidar elastic return is the result of both aerosol and molecular backscattering as well of aerosol extinction at all operating wavelengths. Molecular extinction also contributes but in a negligible way. Raman lidar return is the result of molecular backscattering and aerosol extinction as aerosol scattering is at a different wavelength than the Raman return wavelength and, therefore, not received by the Raman channel.
is volumetric extinction coefficient; and L is geometric distance between emitter and receiver.
The transmitted light is partially reflected or scattered back to the instrument. Radiation (photons) backscattered by the target is collected by a telescope, used as a receiver, and processed to yield information about the observed target. The processing consists of a spectral selection step, made by using a combination of optical elements, and a detection phase operated by means of different devices, such as photomultipliers or avalanche photodiodes, depending on the detected wavelength. The detectors convert the radiation in output electrical signals that, suitably processed, provide vertical profiles of the atmospheric properties as well as the concentration of atmospheric constituents.
Light scattering in the atmosphere includes a large variety of elastic and inelastic processes. The backscattered lidar signal typically consists of elastic scattering from both molecules and particles and of inelastic scattering due to rotational Raman transition in molecules. Lidar elastic return is the result of both aerosol and molecular backscattering as well of aerosol extinction at all operating wavelengths. Molecular extinction also contributes but in a negligible way. Raman lidar return is the result of molecular backscattering and aerosol extinction as aerosol scattering is at a different wavelength than the Raman return wavelength and, therefore, not received by the Raman channel.
2 Molecular scattering
Atmospheric molecules, though much smaller than the wavelengths of light, provide a contribution to the radiation backscattered by the atmosphere. Because molecules are smaller than the wavelength typically used in lidar system (ranging between 266 nm and 2 µm), they scatter short wavelengths (which are more nearly comparable to the size of the molecules) better than long wavelengths (Measures, 1992). Molecular scattering occurs under the Rayleigh scattering regime, i.e when the size of the scatterers 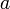 is much lower than the radiation wavelength
is much lower than the radiation wavelength 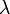 , i.e.
, i.e. 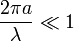 . Rayleigh scattering has a simple classical origin: the electrons in the atoms, molecules or small particles radiate like dipole antennas when they are forced to oscillate by an applied electromagnetic field (Miles, 2001).
Scattering from molecules is of major importance for lidar since the signal from the molecules can be used as a lidar calibration source. Lidar calibration is required for obtaining the system constant needed for particle backscattering coefficient profile retrievals. The conventional calibration approach is to normalize the lidar return to a given molecular reference value in the upper troposphere or stratosphere. This is challenging to apply in the near-IR because of the weak molecular scattering and, above all for ceilometers, of the low signal-to-noise ratio. Moreover, the uncertainty due to the use of a calibration value of the molecular scattering equal to zero (i.e. no aerosol scattering), that is often considered in the signal inversion, can be furthermore critical at infrared wavelengths (larger than 35%), while at lower wavelengths the uncertainty in much lower (within 10 %).
. Rayleigh scattering has a simple classical origin: the electrons in the atoms, molecules or small particles radiate like dipole antennas when they are forced to oscillate by an applied electromagnetic field (Miles, 2001).
Scattering from molecules is of major importance for lidar since the signal from the molecules can be used as a lidar calibration source. Lidar calibration is required for obtaining the system constant needed for particle backscattering coefficient profile retrievals. The conventional calibration approach is to normalize the lidar return to a given molecular reference value in the upper troposphere or stratosphere. This is challenging to apply in the near-IR because of the weak molecular scattering and, above all for ceilometers, of the low signal-to-noise ratio. Moreover, the uncertainty due to the use of a calibration value of the molecular scattering equal to zero (i.e. no aerosol scattering), that is often considered in the signal inversion, can be furthermore critical at infrared wavelengths (larger than 35%), while at lower wavelengths the uncertainty in much lower (within 10 %).
3 Extinction due to aerosols
The term extinction addresses the loss of light in the atmosphere from a directly transmitted beam. Two different mechanisms contribute to extinction: absorption and scattering. Normally, most of the extinction in the Earth's atmosphere is due to scattering. Most of the aerosol particles are so weakly absorbing that their extinction is almost entirely due to scattering, rather than absorption. However, certain aerosol types, like soot (carbon), are quite efficient absorbers and their extinction is largely due to their absorption power. In terms of refractive index, non absorbing particles are characterized by a negligible value of the imaginary part of the complex refractive index. Aerosol extinction can be retrieved with very few assumptions exploiting the significant advantage coming from the use of Raman backscatter. Raman backscatter occurs when the scattering molecules transit from one energy state to another before reemitting the incident light. This results in scattering at shifted frequency/wavelength equal to the difference (the combination) of the incident light frequency and the frequency gap between the final and the initial energy states of scattering molecules. The frequency/wavelength shift depends on the transition type and has a different value for different types of scattering molecules (Serikov et al., 2009). The fraction of the total energy scattered at that wavelength (i.e., the Raman cross-section) is typically three orders of magnitude smaller than for elastic scattering, which allows its practical application to remote sensing of only the most abundant molecules in the atmosphere, like nitrogen or water vapor.
4 Optical properties of aerosol and clouds
Lidar measurements are able to characterize optical properties of aerosol and clouds. Optical properties can be divided in extensive and intensive: extensive properties depend on both the nature and the amount of the aerosol, while intensive properties are independent of aerosol amount, depending only on the nature of the specific aerosol type.
Extensive properties
Optical extensive properties are the extinction coefficient and the backscattering coefficient.
The extinction coefficient 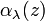 is a measure of attenuation of the light passing through the atmosphere due to the scattering and absorption by aerosol particles.
is a measure of attenuation of the light passing through the atmosphere due to the scattering and absorption by aerosol particles. 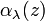 is the fractional depletion of radiance per unit path length (also called attenuation especially in reference to radar frequencies). It has units of
is the fractional depletion of radiance per unit path length (also called attenuation especially in reference to radar frequencies). It has units of 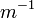 . The extinction coefficient is a combination of the scattering coefficient
. The extinction coefficient is a combination of the scattering coefficient 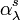 and the absorption coefficient
and the absorption coefficient 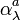 of molecules (mol) and aerosol particles (par):
of molecules (mol) and aerosol particles (par):
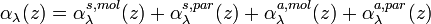 [Eq.1]
[Eq.1]
where z is the altitude range and lidar is pointing in the zenith viewing direction.
The backscatter coefficient 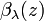 is a measure of the scattering in the backward direction ( i.e. towards the incident direction, at an scattering angle of 180 deg) for the light encountering the atmospheric aerosol particles.
is a measure of the scattering in the backward direction ( i.e. towards the incident direction, at an scattering angle of 180 deg) for the light encountering the atmospheric aerosol particles.
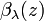 for elastic signals (
for elastic signals (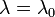 ) can be summed up from the backscatter coefficients of molecules and particles:
) can be summed up from the backscatter coefficients of molecules and particles:
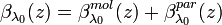 [Eq.2]
[Eq.2]
The backscattering coefficients of the molecular atmosphere as well as of the aerosol particles can be calculated from the number density of the scatterers 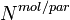 , their scattering cross-section
, their scattering cross-section 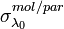 , and the phase function
, and the phase function 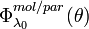 for the scattering angle
for the scattering angle 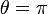 :
:
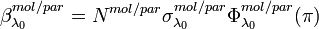 [Eq.3]
[Eq.3]
The column optical depth is also a variable ofter used to describe aerosol and clouds properties over the the full atmospheric column, and it is defined as the integral of the particle extinction coefficient from the ground to the top of the atmosphere (TOA):
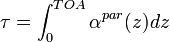 [Eq.4]
[Eq.4]
This definition allows to include also contribution from stratospheric aerosol if present.
Intensive properties
The particle lidar ratio is defined as the ratio of the particle extinction coefficient and the particle backscattering coefficient:
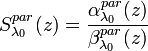 [Eq.5]
[Eq.5]
The lidar ratio can be derived only from profiles of 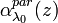 and
and 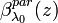 determined in an independent way and with the same time and height resolutions. This can be obtained using the Raman technique, described in section 3.2. In the case of aerosol, lidar ratio can be also estimated using the combination of co-located elastic lidar and sun photometer measurements (Mattis et al., 2004). In case of clouds at infrared wavelengths, as reported in Hogan et al. (2004), according to the Mie theory, droplet size distributions with median volume diameters in the range 5-50 µm have an approximately constant lidar ratio at 18.75 sr.
The Angström coefficient indicates the aerosol extinction coefficient dependence on the wavelength, and it is defined as (Angström, 1929):
determined in an independent way and with the same time and height resolutions. This can be obtained using the Raman technique, described in section 3.2. In the case of aerosol, lidar ratio can be also estimated using the combination of co-located elastic lidar and sun photometer measurements (Mattis et al., 2004). In case of clouds at infrared wavelengths, as reported in Hogan et al. (2004), according to the Mie theory, droplet size distributions with median volume diameters in the range 5-50 µm have an approximately constant lidar ratio at 18.75 sr.
The Angström coefficient indicates the aerosol extinction coefficient dependence on the wavelength, and it is defined as (Angström, 1929):
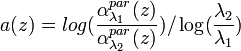 [Eq.6]
[Eq.6]
where 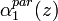 and
and 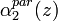 are the aerosol extinction profiles relative to a couple of wavelength (
are the aerosol extinction profiles relative to a couple of wavelength (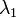 and
and 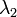 ). As the lidar ratio, the Angström coefficient is not dependent on the aerosol concentration, but it is related to aerosol microphysical properties. It is inversely proportional to the particle size and depends on the complex refractive index of the particles. Lidar depolarization technique is a well-established method to distinguish water phase in clouds, like cirrus and mixed–phase clouds. Two different parameters can be provided with the lidar measurements (Freudenthaler et al., 2009): the linear volume depolarization ratio,
). As the lidar ratio, the Angström coefficient is not dependent on the aerosol concentration, but it is related to aerosol microphysical properties. It is inversely proportional to the particle size and depends on the complex refractive index of the particles. Lidar depolarization technique is a well-established method to distinguish water phase in clouds, like cirrus and mixed–phase clouds. Two different parameters can be provided with the lidar measurements (Freudenthaler et al., 2009): the linear volume depolarization ratio,
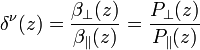 [Eq.7]
[Eq.7]
and the particle linear depolarization ratio,
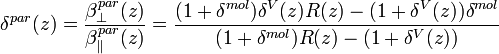 [Eq.8]
[Eq.8]
where 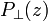 and
and 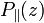 are the measured perpendicular and parallel backscatter radiation intensities from the height z with respect to the transmitter polarization axis;
are the measured perpendicular and parallel backscatter radiation intensities from the height z with respect to the transmitter polarization axis; 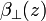 and
and 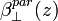 are the total and the particle volume backscattering coefficient from the height z, respectively, with a polarization perpendicular to the polarization of the laser source;
are the total and the particle volume backscattering coefficient from the height z, respectively, with a polarization perpendicular to the polarization of the laser source; 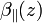 and
and 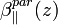 are the total and the particle volume backscattering coefficient from the height z, respectively, with a polarization parallel to the polarization of the laser source;
are the total and the particle volume backscattering coefficient from the height z, respectively, with a polarization parallel to the polarization of the laser source; 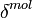 is the height independent linear depolarization ratio of air molecules defined as,
is the height independent linear depolarization ratio of air molecules defined as,
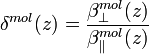 [Eq.9]
[Eq.9]
Finally R(z) is the backscatter ratio, i.e the ratio of the total backscatter coefficient to the molecular component,
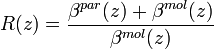 [Eq.10]
[Eq.10]
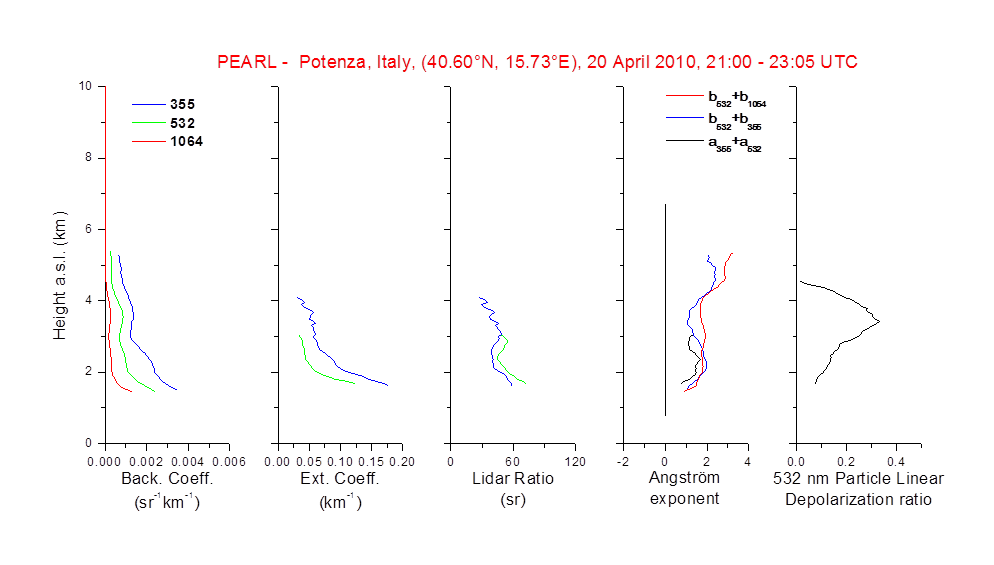
Figure 1: Example of the retrieval of extensive and intensive optical properties obtained with PEARL (Potenza EArlinet Raman Lidar) multi-wavelength lidar system operative at Potenza, Italy, in the frame of EARLINET (European Aerosol Research LIDar NETwork).
The estimation of 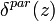 and
and 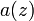 represent the added value of lidar profiling measurements towards the typing of observed particles as a function of the range. The study of depolarization allows us to obtain important information about the particle shape: along with the multi-wavelength backscattering and extinction measurements and the information provided by isentropic back-trajectories, the aerosol depolarization ratio allows to discriminate the nature of the observed particles and to classify them with respect to the source regions. Moreover, observations of the linear depolarization ratio at several wavelengths may be used in retrieval schemes (Dubovik et al., 2006) to improve the estimation of the microphysical properties of dust from optical measurements (Wiegner et al., 2008).
An example of the retrieval of extensive and intensive optical properties obtained with PEARL (Potenza EArlinet Raman Lidar) multi-wavelength lidar system operative at Potenza, Italy, in the frame of EARLINET (European Aerosol Research LIDar NETwork) is reported in Figure 1. The retrieval is referred to the observation to the aerosol outbreak over Europe due to the volcanic eruption of Eyjafjallajökull, a small volcano under Iceland’s ice cap (Mona et al., 2012).
represent the added value of lidar profiling measurements towards the typing of observed particles as a function of the range. The study of depolarization allows us to obtain important information about the particle shape: along with the multi-wavelength backscattering and extinction measurements and the information provided by isentropic back-trajectories, the aerosol depolarization ratio allows to discriminate the nature of the observed particles and to classify them with respect to the source regions. Moreover, observations of the linear depolarization ratio at several wavelengths may be used in retrieval schemes (Dubovik et al., 2006) to improve the estimation of the microphysical properties of dust from optical measurements (Wiegner et al., 2008).
An example of the retrieval of extensive and intensive optical properties obtained with PEARL (Potenza EArlinet Raman Lidar) multi-wavelength lidar system operative at Potenza, Italy, in the frame of EARLINET (European Aerosol Research LIDar NETwork) is reported in Figure 1. The retrieval is referred to the observation to the aerosol outbreak over Europe due to the volcanic eruption of Eyjafjallajökull, a small volcano under Iceland’s ice cap (Mona et al., 2012).
5 Inversion methods
Lidar equation is the way to relate the light power backscattered by the atmospheric target with the signal collected by the lidar receiver. In a general form, lidar equation can be written as
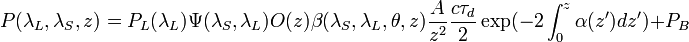 [Eq.11]
[Eq.11]
where:
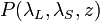 is the backscattered power received from the distance
is the backscattered power received from the distance 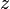 from the source (zenith pointing), at a specific polarization and wavelength
from the source (zenith pointing), at a specific polarization and wavelength 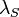 , due to the scattering of the laser wavelength
, due to the scattering of the laser wavelength 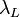 ;
;
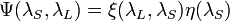 is transmission of the lidar receiver, given by
is transmission of the lidar receiver, given by 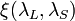 that is the optical efficiency of the lidar receiver, including such factors as the reflectivity of the telescope and the transmission of the conditioning optics, while
that is the optical efficiency of the lidar receiver, including such factors as the reflectivity of the telescope and the transmission of the conditioning optics, while 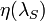 is the quantum efficiency of the receiver and detection parts;
is the quantum efficiency of the receiver and detection parts;
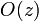 is the system overlap function;
is the system overlap function;
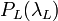 is the output laser power at the wavelength
is the output laser power at the wavelength 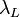 ;
;
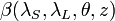 is the volume scattering coefficient at the distance
is the volume scattering coefficient at the distance 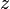 and at an angle
and at an angle 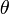 and represents the probability that a transmitted photon is backscattered by the atmosphere into a unit solid angle (
and represents the probability that a transmitted photon is backscattered by the atmosphere into a unit solid angle (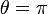 );
);
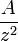 is the probability that a photon scattered from the distance
is the probability that a photon scattered from the distance 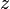 is collected by the receiving telescope of surface
is collected by the receiving telescope of surface 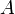 ;
;
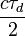 represents the sounding vertical resolution, where
represents the sounding vertical resolution, where  and
and 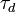 are respectively the light speed and the dwell time (i.e. the laser duration pulse);
are respectively the light speed and the dwell time (i.e. the laser duration pulse);
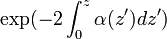 is the two-way transmissivity of the light from laser source to the distance
is the two-way transmissivity of the light from laser source to the distance 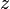 and from distance
and from distance 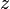 to the receiver;
to the receiver;
 is the contribution power return due to the background photons.
To use [Eq.11] for the inversion of the backscattered radiation and to retrieve the atmospheric parameters, the approximation of single and independent scattering is needed: this means that a photon is scattered only once by the atmospheric constituents and that these are adequately separated and are randomly moving. Thus, the contributions to the total scattered energy by many targets have no phase relation and the total intensity is simply the sum of the intensities scattered from each target.
The inversion of lidar equation can be performed using different methods depending on the availability of the elastic signal only or also the Raman signal. The methods more frequently applied are described in the next section.
is the contribution power return due to the background photons.
To use [Eq.11] for the inversion of the backscattered radiation and to retrieve the atmospheric parameters, the approximation of single and independent scattering is needed: this means that a photon is scattered only once by the atmospheric constituents and that these are adequately separated and are randomly moving. Thus, the contributions to the total scattered energy by many targets have no phase relation and the total intensity is simply the sum of the intensities scattered from each target.
The inversion of lidar equation can be performed using different methods depending on the availability of the elastic signal only or also the Raman signal. The methods more frequently applied are described in the next section.
Backscattering coefficients from an elastic signal
The calculation of the backscattering coefficients from an elastic signal can be performed using different methods. In the following the Klett-Fernald and iterative methods are described.
Klett method
One of the most common method to derive backscatter coefficient form elastic lidar measurements is the so-called Klett inversion method [Ansmann et al., 1990]. This method, however, has the disadvantage that two physical quantities, the aerosol backscatter and extinction coefficients must be determined from only the elastic backscatter. This is not possible without assumptions about the relationship between the two and an estimate of a reference value of the aerosol extinction.
In one of the possible variant of Klett method [Klett, 1981, Fernald, 1984], 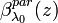 can be obtained as
can be obtained as
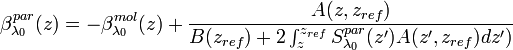 [Eq.12]
[Eq.12]
In the [Eq.12], we have:
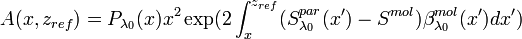 with
with 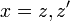 ,
,
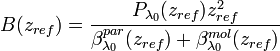 ,
,
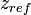 is a reference range assumed in an aerosol-free region.
is a reference range assumed in an aerosol-free region.
Iterative method
The iterative method is described, e.g., by Di Girolamo et al. [1999]. The particle backscatter coefficient
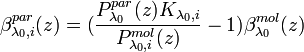 [Eq.13]
[Eq.13]
is calculated in the i-th iteration step from the measured, pre-processed, overlap-corrected signal and an estimated molecular signal, expressed as:
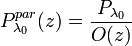
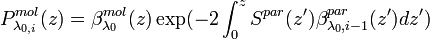
 is a calibration factor and can be determined in an aerosol-free region
is a calibration factor and can be determined in an aerosol-free region 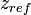 :
:
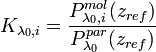
A proper profile 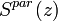 or a height-independent value
or a height-independent value 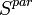 of the lidar ratio has to be assumed. In an initial step the molecular signal
of the lidar ratio has to be assumed. In an initial step the molecular signal 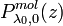 is estimated with the assumption
is estimated with the assumption 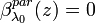 and is then used to derive an initial value of
and is then used to derive an initial value of 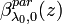 . In the following iteration step i the backscatter coefficient
. In the following iteration step i the backscatter coefficient 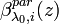 is calculated from a molecular signal which is estimated from the previous backscatter profile
is calculated from a molecular signal which is estimated from the previous backscatter profile 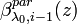 . This procedure is repeated until the difference between
. This procedure is repeated until the difference between 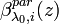 and
and 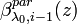 is smaller than a certain threshold.
is smaller than a certain threshold.
General considerations
The retrieval of the backscattering coefficient using only the elastic signals is affected by sources of uncertainties. Over those affecting all the lidar retrievals, there are two additional large sources of uncertainty due to:
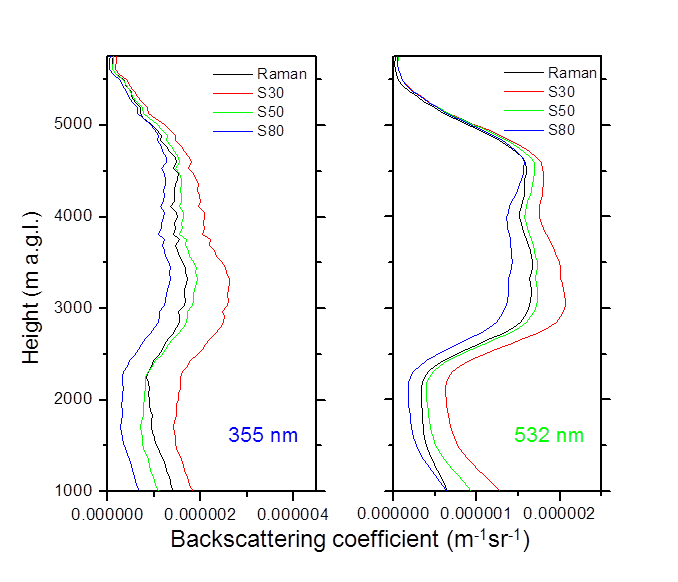
1. uncertainty due to the assumption of a particle lidar ratio (profile); this uncertainty can easily exceed 20% [Sasano et al., 1985], as shown in figure 2, where profiles of the backscattering coefficient obtained using the iterative method assuming a lidar ratio equal to 30, 50 and 80 sr, respectively, are compared with the results of the Raman/Elastic combined retrieval.
2. uncertainty in the lowest part of the profile due to the incomplete overlap between laser beam and receiver field of view (Mattis et al., 2007) and the necessity to correct measured signals with the overlap function 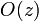 .
.
Figure 2: Example of the effect of lidar ratio assumption in the iterative method for the inversion of lidar equation. Black line is the profile obtained using the Raman/elastic combined technique, red line is the profile obtained using the iterative method with a lidar ratio of 30 sr, green line is the same with a lidar ratio of 50 sr, and red line with a lidar ratio of 80 sr. Left panel reports the comparison at 355 nm and the right panel the comparison at 532 nm.
Backscatter and extinction coefficients using elastic and Raman signals
The Raman/elastic combined technique provides independent estimations of the aerosol backscattering and extinction profiles avoiding the assumptions necessary to invert the lidar equation in the elastic case (Pappalardo et al., 2004). In this case, the molecules change their initial states to different final states and the scattered light experiences a frequency shift due to vibrational-rotational Raman shift or pure rotation Raman shift. The inelastic Raman backscatter signals are affected by the aerosol attenuation but they are independent on the aerosol backscatter, then it is possible to retrieve the aerosol extinction coefficient 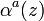 , for example using as reference the nitrogen (or also the oxygen) Raman return. In fact, the nitrogen has a well-known distribution in the atmosphere. Therefore, making the logarithm and the derivative of the [Eq. 11], we obtain:
, for example using as reference the nitrogen (or also the oxygen) Raman return. In fact, the nitrogen has a well-known distribution in the atmosphere. Therefore, making the logarithm and the derivative of the [Eq. 11], we obtain:
![\frac{d}{dz}\Bigg[\ln\Bigg(\frac{n_{R}(z)}{P(\lambda_{R},z)z^{2}}\Bigg)+\ln\Bigg(P_{L}A_{0}\frac{c\tau_{d}}{2}\Psi(\lambda_{L},\lambda_{R})\frac{d\sigma(\lambda_{R})}{d\Omega}\Bigg)\Bigg]=\alpha_{\lambda_{L}}^{mol}(z)+\alpha_{\lambda_{L}}^{par}(z)+\alpha_{\lambda_{R}}^{mol}(z)+\alpha_{\lambda_{R}}^{par}(z)](/wiki.eg-climet.org/images/math/6/6/3/663d547706c82a6ae32543cb5c96a35b.png)
and then solving with respect to the extinction of particles
![\alpha_{\lambda_{L}}^{par}(z)+\alpha_{\lambda_{R}}^{par}(z)=\frac{d}{dz}\Bigg\{\ln\Bigg[n_{R}(z)/P_{\lambda_{R}}(z)z^{2}\Bigg]\Bigg\}-\alpha_{\lambda_{L}}^{mol}(z)-\alpha_{\lambda_{R}}^{mol}(z)](/wiki.eg-climet.org/images/math/e/f/9/ef91db416e3939bd1cc61375e20843cf.png) [Eq.14]
[Eq.14]
where we have made explicit the nitrogen backscattering cross-section as the product of the differential backscattering cross-section 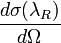 and the number of scatters
and the number of scatters 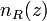 . The wavelength dependence of the aerosol extinction coefficient is described by the Ǻngström coefficient,
. The wavelength dependence of the aerosol extinction coefficient is described by the Ǻngström coefficient, 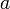 , defined from the relation
, defined from the relation 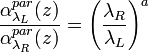 . Ansmann (1992) showed that this dependence is lower than 1% and thus it can be considered as negligible. Finally, resolving the [Eq.14] with respect to
. Ansmann (1992) showed that this dependence is lower than 1% and thus it can be considered as negligible. Finally, resolving the [Eq.14] with respect to 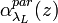 , we have:
, we have:
![\alpha_{\lambda_{L}}^{par}(z)=\frac{\frac{d}{dz}\Bigg\{\ln\Bigg[n_{R}(z)/P_{\lambda_{R}}(z)z^{2}\Bigg]\Bigg\}-\alpha_{\lambda_{L}}^{mol}(z)-\alpha_{\lambda_{R}}^{mol}(z)}{1+\Bigg(\frac{\lambda_{L}}{\lambda_{R}}\Bigg)^{a}}](/wiki.eg-climet.org/images/math/e/7/c/e7ce704d4f47dafe03a99c6f64d174d2.png) [Eq.15]
[Eq.15]
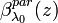 can be derived directly from the ratio of the Raman signal at
can be derived directly from the ratio of the Raman signal at 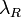 and the elastic signal at
and the elastic signal at 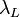 (Ansmann et al, 1992) as:
(Ansmann et al, 1992) as:
![\beta_{\lambda_{L}}^{par}(z)=-\beta_{\lambda_{L}}^{mol}(z)+\Big[\beta_{\lambda_{L}}^{par}(z_{ref})+\beta_{\lambda_{L}}^{mol}(z_{ref})\Big]\frac{O_{\lambda_{R}}(z)P_{\lambda_{R}}(z_{ref})P_{\lambda_{L}}(z)\beta_{\lambda_{L}}^{mol}(z)}{O_{\lambda_{L}}(z)P_{\lambda_{L}}(z_{ref})P_{\lambda_{R}}(z)\beta_{\lambda_{L}}^{mol}(z_{ref})}\exp(C)](/wiki.eg-climet.org/images/math/e/4/9/e496edac67fd3ba7923812999b604d24.png) [Eq.16]
[Eq.16]
with 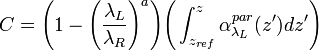 .
. 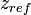 is a reference altitude assumed aerosol free.
is a reference altitude assumed aerosol free.
Alternatively, Ferrare et al. [1998] suggested another way to derive 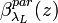 calculating first the backscattering ratio:
calculating first the backscattering ratio:
![R(z)=\frac{\beta^{par}(z)+\beta^{mol}(z)}{\beta^{mol}(z)}=F^{\beta}\frac{O_{\lambda_{R}}(z)P_{\lambda_{L}}(z)}{O_{\lambda_{L}}(z)P_{\lambda_{R}}(z)}\exp\Bigg[\Bigg(1-\Bigg(\frac{\lambda_{L}}{\lambda_{R}}\Bigg)^{a}\Bigg)\int_{0}^{z}\alpha_{\lambda_{L}}^{par}(z^{\prime})dz^{\prime}\Bigg]](/wiki.eg-climet.org/images/math/5/d/4/5d4033c7eae613fa9a6d2521ec29295c.png) [Eq.17]
[Eq.17]
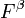 is a calibration factor. Then
is a calibration factor. Then 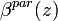 can be derived as:
can be derived as:
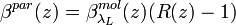
The advantage of this method is that it theoretically allows for an absolute calibration of the lidar system. If the calibration factor 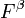 is derived once under optimal atmospheric conditions (clean free troposphere), it can be applied to all other measurements under arbitrary conditions as long as the system configuration does not change.
is derived once under optimal atmospheric conditions (clean free troposphere), it can be applied to all other measurements under arbitrary conditions as long as the system configuration does not change.
6 References
Ångström, A., On the atmospheric transmission of Sun radiation and on dust in the air, Geogr. Ann. Dtsch., 12, 156–166, 1929.
Ansmann, A, M Riebesell, and C Weitkamp. Measurements of atmospheric aerosol extinction profiles with Raman lidar, Optics Letters 15:746-748, 1990.
Ansmann, A., Wandinger, U., Riebesell, M., Weitkamp, C., and Michaelis, W.: Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined Raman elastic-backscatter lidar, Appl. Optics, 31, 7113–7131, 1992.
Dubovik, O., Sinyuk, A., Lapyonok, T., Holben, B. N., Mishchenko, M. and co-authors. Application of spheroid models to account for aerosol particle nonsphericity in remote sensing of desert dust. J. Geophys. Res. 111, doi:10.1029/2005JD006619, 2006.
Freudenthaler, V., et al., Depolarization ratio profiling at several wavelengths in pure Saharan dust during SAMUM 2006, Tellus, Ser.B, 61, 165–179, 2009.
Di Girolamo, P., P. F. Ambrico, A. Amodeo, A. Boselli, G. Pappalardo, and N. Spinelli, Aerosol observations by lidar in the nocturnal boundary layer, Appl. Opt., 38 (21), 4585–4595, 1999.
Fernald, F. G., Analysis of atmospheric lidar observations: some comments, Appl. Opt., 23 (5), 652–653, 1984.
Ferrare, R. A., S. H. Melfi, D. N. Whiteman, K. D. Evans, and R. Leifer, Raman lidar measurements of aerosol extinction and backscattering: 1. Methods and comparisons, J. Geophys. Res., 103, 19,663–19,672, 1998.
Fiocco, G.; and Smullin, L. D., (60-140 km) by Optical Radar. Detection of Scattering Layers in the Upper Atmosphere Nature I;ae, I275 (1963).
Klett, J. D., Stable analytic inversion solution for processing lidar returns, Appl. Opt., 20, 211–220, 1981.
Mattis, I., A. Ansmann, D. Müller, U. Wandinger, and D. Althausen, Multiyear aerosol observations with dual-wavelength Raman lidar in the framework of EARLINET, J. Geophys. Res., 109, D13203, doi:10.1029/2004JD004600, 2004.
Mattis , I., A. Chaikovsky, A. Amodeo, G. D’Amico, and G. Pappalardo, Assessment report of existing calculus subsystems used within EARLINET-ASOS, Tech. rep., EARLINET ASOS, 2007.
Measures, R. M., Laser remote sensing: fundamentals and applications, 2 ed., 510 pp., Krieger Publishing Company, Malabar, Florida, 1992.
Miles, R.B., W.R. Lempert, J.N. Forkey, Laser Rayleigh scattering, Meas. Sci. Technol., 12, pp. R33–R51, 2001.
Mona, L., Amodeo, A., D’Amico, G., Giunta, A., Madonna, F., and Pappalardo, G.: Multi-wavelength Raman lidar observations of the Eyjafjallaj¨okull volcanic cloud over Potenza, southern Italy, Atmos. Chem. Phys., 12, 2229–2244, doi:10.5194/acp-12-2229-2012, 2012.
Pappalardo, G., et al., Aerosol lidar intercomparison in the framework of the EARLINET project. 3. Raman lidar algorithm for aerosol extinction, backscatter, and lidar ratio, Appl. Opt., 43, 5370–5385, 2004.
Sasano, Y., E. V. Browell, and S. Ismail, Error caused by using a constant extinction/backscatter ratio in the lidar solution, Appl. Opt., 24, 3929–3932, 1985.
Wiegner, M., Gasteiger, J., Kandler, K.,Weinzierl, B., Rasp, K. and coauthors, Numerical simulations of optical properties of Saharan dust aerosols with special emphasis on the linear depolarization ratio. Tellus 61B, doi:10.1111/j.1600-0889.2008.00381.x., 2008.